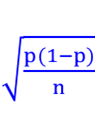L' ANALYSE DESCRIPTIVE
L’ analyse descriptive est la première étape d’une analyse statistique. Elle permet de résumer les données dans un tableau descriptif avec des paramètres mathématiques comme la moyenne, l’effectif ou fréquence, la médiane, l’écart type (ou l’erreur standard), le minimum et le maximum.
Sommaire
L’ analyse descriptive est très importante lors d’une analyse. Elle nous permet d’observer d’une manière synthétique les variables d’intérêt et de comparer visuellement leurs paramètres selon des critères ou par groupes de sujets. Ainsi, nous pouvons détecter des informations précieuses tel que la distribution des données, leur homogénéité et l’existence des données manquantes, aberrantes et les extrêmes.
Résultats de l'analyse descriptive
La majorité d’entre nous, connait et sait comment calculer une moyenne. Mais qu’en est-il de l’écart type, la variance ou l’erreur standard ? Ces derniers paramètres sont aussi importants que la moyenne pour présenter les résultats d’une étude. La moyenne résume et donne un ordre de grandeur du critère étudié. L’écart type ou la variance quand à eux, permettent de montrer la qualité et l’homogénéité des données de l’échantillon sur le quelle elle se base l’analyse statistique.
Nous savons tous que les résultats d’une étude publiée sont sous forme d’un tableau décrivant le critère étudié avec des paramètres descriptif. Et s’il s’agit d’un facteur quantitatif par exemple, la moyenne doit être représentée pour chaque groupe et elle est accompagnée de son écart type. Une moyenne sans son écart type n’a pas de valeur indicative.
Maintenant que l’on connait l’intérêt l’intérêt des paramètres descriptifs lors d’une analyse statistique, nous allons exposer chacun des plus importants d’entre eux avec leur formule mathématique. Mais aussi avec la fonction Excel qui permet de les calculer d’une manière automatique.
Les paramètres descriptifs
Les paramètres descriptifs sont calculés et représentés selon le type de variable étudiée.
Les plus importants et représentés dans les tableaux statistiques sont:
Moyenne, médiane, mode, quartiles, variance, écart type, min et max, coefficient de variation et Intervalles de Confiance IC. Pour les variables quantitatives.
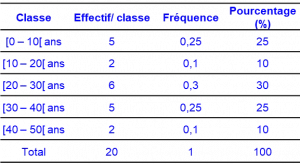
Effectif, fréquence relative, pourcentage, écart type de la proportion, IC de la proportion. Pour les variables qualitatives.
Analyse descriptive d'un critère qualitatif
Effectif ou Fréquence absolue ni
Est le nombre de fois ou une valeur apparait pour le caractère étudié. C’est aussi le nombre d’individu ayant la même valeur dans la variable étudiée.
La somme des fréquences absolues ni = n (Nombre total de sujets)
Fréquence relative : Nombre d’individu ayant la même valeur pour le caractère étudié (ni) par rapport au nombre total d’individu (n).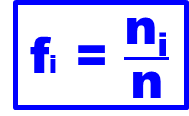
Pourcentage : fréquence relative exprimée en pourcentage (%) = (x100)
Analyse descriptive d'un critère quantitatif
Calcul de la moyenne
La médiane
La Moyenne est la somme algébrique des valeurs observées divisées par le nombre total des observations/sujets. Elle est notée : M , m , µ ou x ̅
C’est le paramètre le plus utilisée pour décrire les variables quantitatives. Elle est plus explicite dans le cas où les données ont une distribution symétrique (Homogène/ même ordre de grandeur). Et elle s’interprète mieux pour les tests statistiques. Par contre la moyenne est très sensible au valeurs extrêmes.
Fonction Excel : =moyenne(A1:A40)
La médiane et la valeur qui divise la série des données en deux parties ou effectifs égaux.
Pour la calculer manuellement il faut trier les observations par ordre croissant ou décroissant, puis prendre la valeur qui correspond au sujet médian, si l’effectif N est impair.
Si l’effectif N est pair, on prend dans ce vas là la moyenne des deux valeurs médianes.
La médiane est moins sensibles aux valeurs anormales (extrêmes). Par contre elle est moins utilisée pour la significativité des tests statistiques.
On utilise souvent la médiane pour les petits effectifs, quant les données ne suivent pas une distribution normale ou quand il y a des valeurs extrêmes très importants.
Fonction Excel : =médiane(A1:A40)
Les paramètres descriptifs de dispersion
Comme leurs noms l’indique, les paramètres de dispersion donnent des informations sur la répartition des données. Ils sont calculés pour les variables quantitatives et mesurent l’homogénéité des valeurs au sein de toute la série.
Par exemple les extrêmes ou valeurs minimale et maximale d’une série de données donnent des informations sur l’étalement des valeurs autour de la médiane.
La variance et l’écart type quand à eux, mesurent la variation de chaque valeur par rapport à la valeur moyenne.
Se sont aussi des indicateurs de la normalité dans le cas d’utilisation d’un test paramétrique.
Les extrêmes, le mode et les quartiles
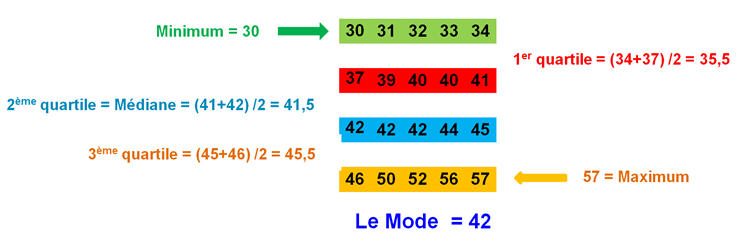
Les extrêmes = minimum et maximum : se sont les deux valeurs extrêmes de la distribution. Ex. Poids Min=30kg ; max=57kg.
Fonction Excel : =min(A1:A40) ; =max(A1:A40)
Etendus (range en anglais) : C’est la différence entre la valeur maximum et minimum. Ex. Range = 57 – 30 = 27kg.
Fonction Excel : =mode(A1:A40)
Mode : est la valeur la plus fréquente dans une série de données. En quelque sorte c’est la valeur dominante dans la série. Mode = 42 kg qui est représenté 3 fois.
Les Quartiles : ou les 3 valeurs qui divise la distribution en quatre partie égales.
Fonction Excel : =quartile(A1:A40;Quartile_Nombre).
Calcul de la Variance
La variance est le paramètre permettant la description de la distribution des données. Elle résume les écarts entre chaque valeur et la valeur moyenne. C’est la moyenne des carrés des écarts de chaque valeur à la valeur moyenne.
Plus la variance est faible, et plus les données sont homogènes et s’approchent de la moyenne.
xi: valeurs des observations
μ: moyenne des observations
n : nombre d’observations
Fonction Excel : =var.s(A1:A40)
Exemple Calcul de la variance des âges de 10 étudiants ?
Calcul de l' écart type
 ou
ou 
Fonction Excel : =STDEV(A1:A40) ou =ecarttype (A1:A40).
Erreur Standard ou Ecart type de la moyenne
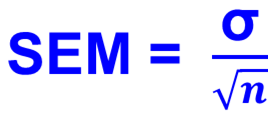
Variance, Ecart type et Erreur Standard du pourcentage
Representations graphiques
Nous pouvons aussi décrire et représenter l’ensemble des données à l’aide de représentations graphiques. Celles -ci nous permettent une première comparaison visuelle plus simple. En effet le on choisit entre les différentes représentations graphiques en fonction du facteur ou de la variable étudiée et de ce que l’on veut expliquer comparer.
Histogramme des fréquences,
Diagramme à secteur ou Camembert,
Polygone de fréquence,
Box plot ou Boite à Moustache,
Nuage de point,
Courbe de tendances des Moyennes.
Si cet article vous a été utile, Merci de le partager
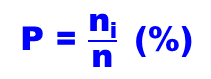




 et
et