Normalité des données - Pourquoi et comment la mesurer ?
Lors d’une étude ou nous voulons comparer entre facteurs quantitatifs, nous pensons tout de suite à utiliser un test T de Student ou une ANOVA. En effet, ce sont bien ces tests qu’il faut privilégier en premier car ce sont des tests puissants. Seulement, ces tests sont des tests paramétriques qui obéissent à la condition de la normalité des données. Cela veut dire que pour pouvoir les appliquer pour une comparaison ou une corrélation, il faut que les données suivent aussi une distribution Normale. Mais qu’est-ce que c’est que la normalité des données et comment faut-il la vérifier ? Nous essayerons d’expliquer dans cet article et de manière la plus simple possible, pourquoi et comment mesurer la normalité des données quantitatives. Nous détaillerons aussi comment réaliser un test formel de normalité pour appliquer un test paramétrique.
Sommaire
Pourquoi mesurer la distribution des données ?
Une des bases d’une analyse statistique consiste à mesurer la distribution des données de la variable d’étude, puis de la comparer à l’un des modèles de distributions théoriques existantes. Les plus importants de ces modèles théoriques sont la loi Normale, la loi Binomiale et la loi de Poisson. Le but de cette mesure est d’appliquer toutes les propriétés mathématiques de ce modèle aux données étudiées. Plus précisément, pour utiliser le test statistique géré par cette loi ainsi que la Table des nombres correspondante. C’est le cas du test T de Student ou l’ANOVA qui sont des tests paramétriques gérés par la loi Normale.
Donc, pour pouvoir utiliser ces tests statistiques, il faut que les données à analyser suivent une distribution normale.
Loi Normale
La loi Normale est l’une des lois les plus importantes utilisées en statistique. Elle s’applique surtout aux variables quantitatives.
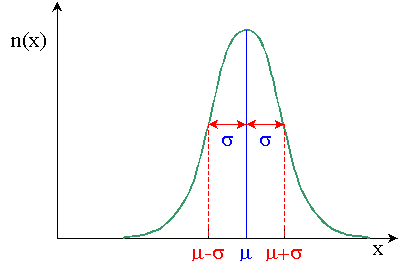
Il est à retenir qu’en biologie, en médecine et en général en sciences de la vie, la majorité des caractères dans la nature suivent une loi normale. Par exemple, la taille des individus, la concentration en globules rouges dans le sang ou le temps d’incubation d’une maladie, suivent une distribution Normale. Cela veut dire que ces caractères chez l’ensemble des individus de la population obéissent à une caractéristique commune. Celle que les mesures fluctuent autour d’une moyenne µ et d’un écart type σ. La représentation graphique des fréquences de ces mesures se présente sous la forme d’une courbe en cloche particulièrement symétrique autour de la moyenne.
Pour mieux comprendre cette notion, nous utiliserons un exemple concret, celui des mesures de la taille (cm) des individus et qui nous servira aussi comme modèle de démonstration.
Exemple Taille des individus en cm
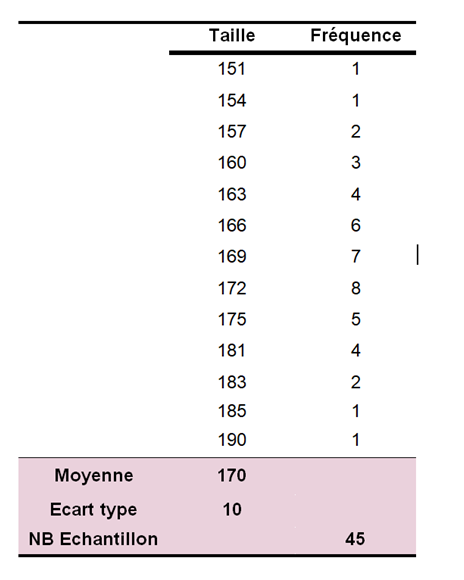
Dans un groupe de 45 sujets pris au hasard, donc dans un échantillon aléatoire, nous mesurons dans un premier temps, leurs tailles en cm. Ensuite, nous calculons la moyenne et l’écart type de cet échantillon: n= 45, moyenne µ= 170 cm et d’écart type σ = 10 cm.
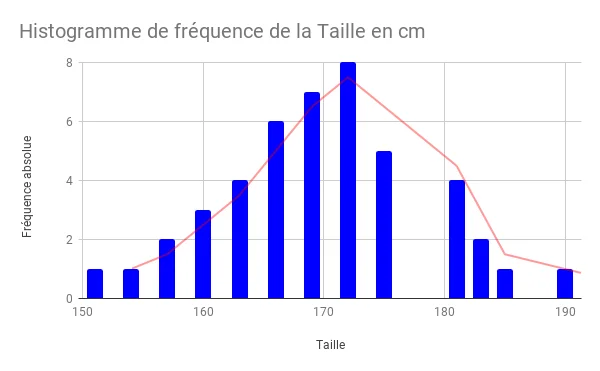
Dans un deuxième temps et pour chaque valeur de la taille de classe = 1 cm, nous calculons la fréquence ou le nombre de sujet. Par la suite, nous traçons l’histogramme de fréquence des différentes classes de la variable Taille. Ci-dessous les données de l’échantillon et l’histogramme de fréquence tracé.
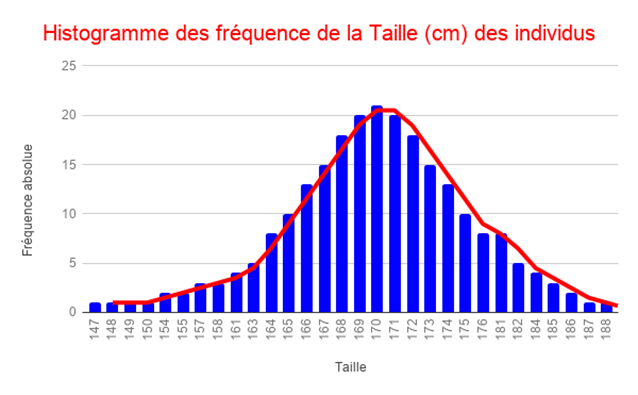
Si nous prenons un échantillon plus grand de 100 sujets, nous réalisons les mêmes étapes décrites précédemment et nous traçons l’histogramme et le polygone de fréquence des tailles des individus (tracé ci-dessous).
De la même manière, nous continuons de tracer les histogrammes d’échantillons de plus en plus grands de 1000 individus, 10000, …., puis de la population entière. Au fur et à mesure que la taille de l’échantillon augmente et que la taille des classes diminue, nous observons que l’histogramme de fréquence devient de plus en plus symétrique et régulier se rapprochant ainsi d’une courbe en cloche. C’est la courbe de la distribution de la loi Normale de moyenne µ=170 cm et d’écart type σ=1cm. cela démontre que la taille des individus dans la population suit une loi normale.
Caractéristiques de la courbe de la loi Normale
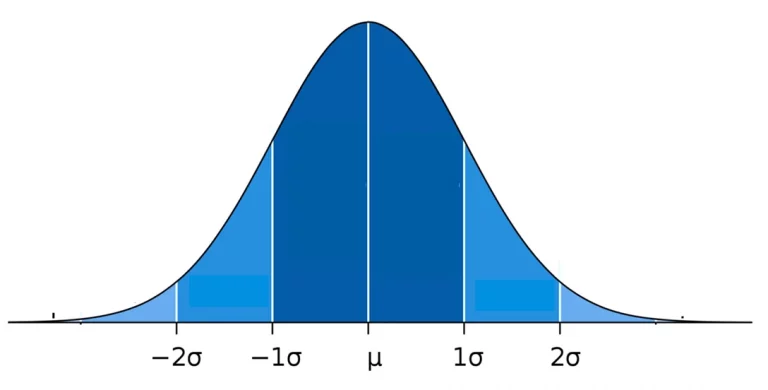
Comme déjà mentionné plus haut, la majorité des caractères en biologie, comme la taille, le poids, la PA, le taux de triglycérides, le QI, la concentration de la vitamine C dans l’orange,…etc. suivent une distribution normale caractérisée par une courbe en cloche symétrique autour d’une moyenne µ et d’un écart type σ.
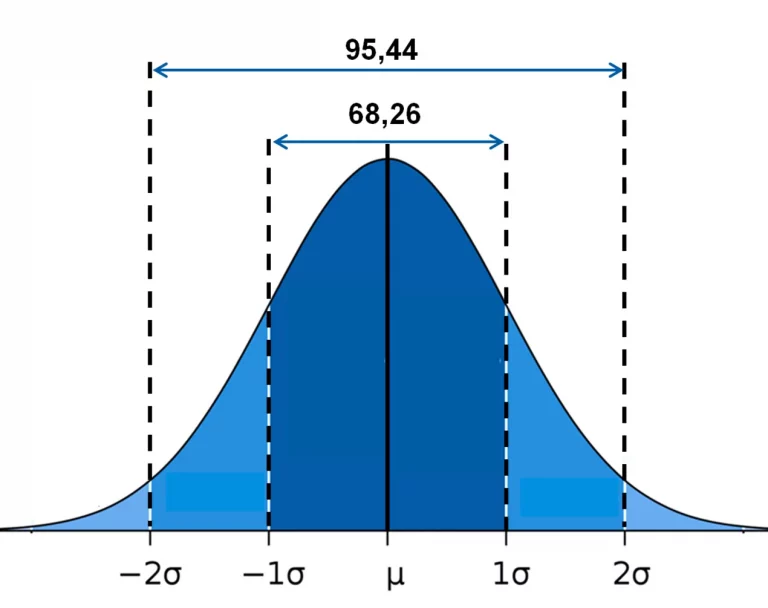
L’aire sous la courbe représente 100% des individus de la population. La majorité des individus, 68,28% de cette population ont une valeur moyenne ± 1 écart type. Et 95% des individus ont une valeur moyenne ± 2 écart types.
En application à notre exemple la Taille (cm), nous pouvons affirmer que 68,28% des sujets adultes de la population mesurent entre 160 cm et 180 cm (µ =170 ± σ =10 cm). Et les 95% de la population mesurent entre 150 et 190 cm. Seulement les 5 % restants ont des mesures au-delà de ces dernières valeurs.
Propriétés de la loi Normale
La loi normale ou loi de Gauss (selon son créateur est Karl Friederich Gauss (1777-1855)) est Centrée autour de la moyenne µ. Sa médiane est égale à sa moyenne.
L’aire compris entre -1,96 σ et +1,96 σ autour de la moyenne représente 95% de l’aire de la courbe.
Son expression mathématique est : 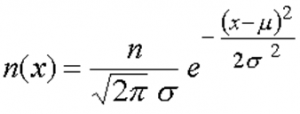
µ = moyenne; σ = écart type; x = valeur de la variable ou du caractère (par ex. Taille de 168,7 cm) et n(x) = Nombre d’individus ayant une valeur (x) de la variable.
Loi Normale centrée réduite
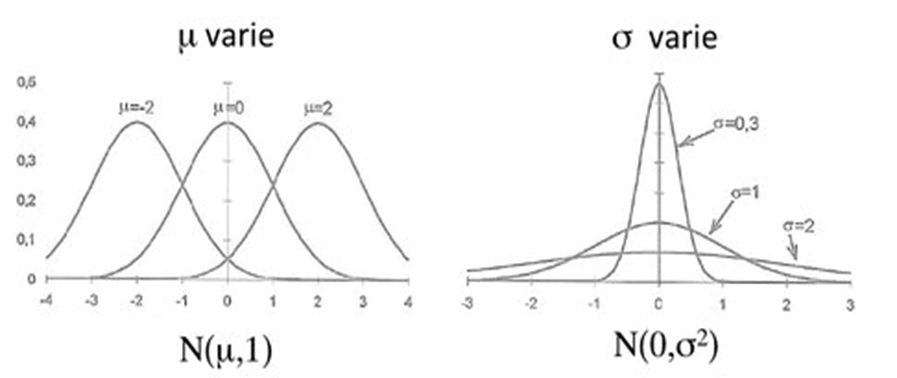
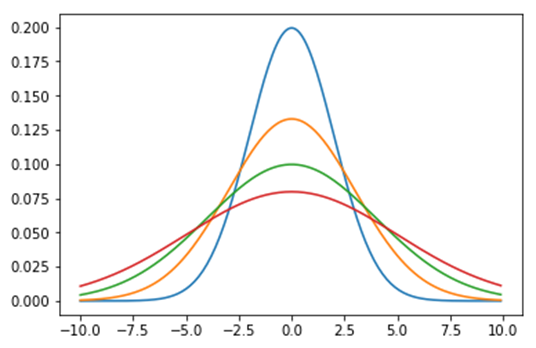
Toutes les variables qui suivent une loi normale sont représentées par une courbe en cloche dont la forme dépend de leurs moyennes et de leurs écarts types.
Afin de normaliser toutes les distributions avec une valeur unique de la moyenne et de son écart type, les statisticiens ont appliqué des transformations mathématiques pour centrer les distributions autour de zéro et ainsi donner la table de Zα de la loi normale centrée réduite.
La nouvelle distribution est appelée donc loi Normale Centrée Réduites et sera en effet centrée autour de la moyenne µ= 0 avec un écart type σ=1.
Propriétés de la loi Normale centrée réduite Z
La loi Z est centrée autour de la valeur moyenne = 0 et d’écart type = 1.
95% des valeurs de Z sont comprises entre -1,96 et + 1,96 (ou -2 et +2).
2,5% des valeurs sont < à -1,96 et 2,5% des valeurs sont > à +1,96.
Plusieurs lois de probabilités sont dérivées de la loi normale. Les plus utilisées en statistiques et qui serviront pour les tests sont:
- Loi du Chi2
- Loi de Student
- Loi de Fisher
Ces informations sont fondamentales pour comprendre tout raisonnement en Biostatistiques. Comme par exemple, l’estimation des paramètres d’une population à partir des paramètres de l’échantillon. La compréhension et l’application des tests statistiques.
Comment mesurer la Normalité des données ?
Plusieurs moyens sont possibles pour estimer et visualiser la normalité des données quantitatives.
Par examen des paramètres descriptifs
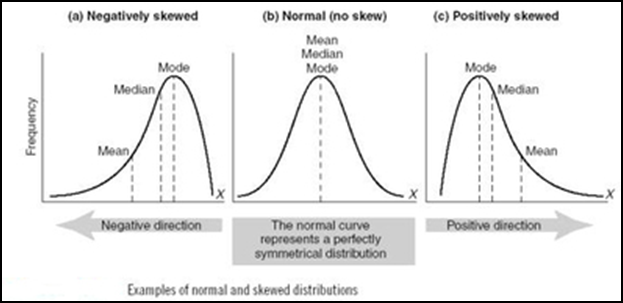
La première méthode consiste à comparer les paramètres descriptifs calculés dans l’échantillon.
Si par exemple la Moyenne = Médiane = Mode, nous pouvons considérer que la distribution des données de l’échantillon suit une loi normale.
C’est aussi le cas si l’intervalle compris entre -1 écart type et +1 écart type contient 2/3 des valeurs.
Mesures graphiques de la Normalité
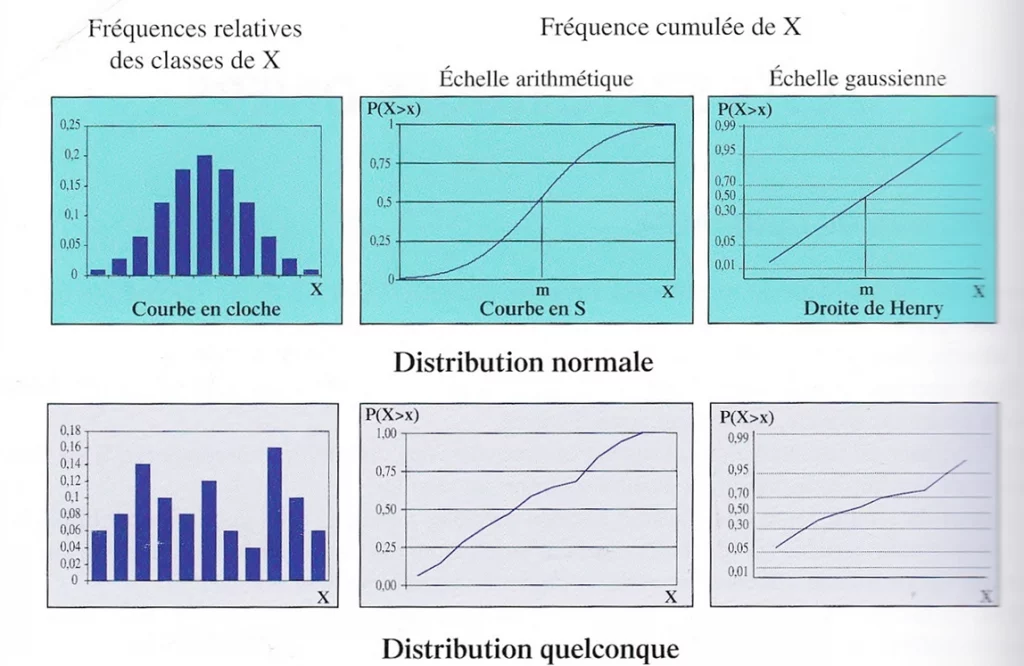
Le deuxième moyen est une évaluation visuelle en examinant l’histogramme représentant les fréquences des classes de la variable étudiée. Si cet histogramme a une forme symétrique autour de la moyenne avec une forme d’une courbe en cloche Gaussienne, alors les données ont une distribution normale.
De la même manière, si les valeurs de la variable sont alignées sur la droite des graphiques QQ-plot et de la droite d’Henri, les données peuvent être considérées comme normales.
Test de Normalité
La troisième méthode de mesure de la normalité des données est par l’utilisation d’un test formel celui de Shapiro-Wilk ou le test de Kolmogorov-Smirnov. Ces tests doivent être réalisés sur un logiciel de statistique.
Test de Normalité de Shapiro-Wilk
Hypothèse nulle H0 : La variable dont provient l’échantillon suit une loi Normale. Versus hypothèse alternative H1 : La variable dont provient l’échantillon ne suit pas une loi Normale.
En réalisant le test de Shapiro-Wilk, nous obtiendrons évidement deux résultats possibles de la p-value:
Soit p-value > 0,05 (avec le niveau de signification alpha=5%), dans ce cas l’hypothèse nulle H0 est acceptée. Nous pouvons conclure que les données suivent une distribution Normale. Soit la p-value est ≤ 0,05. L’hypothèse H0 est rejetée et les données n’ont pas une distribution normale.
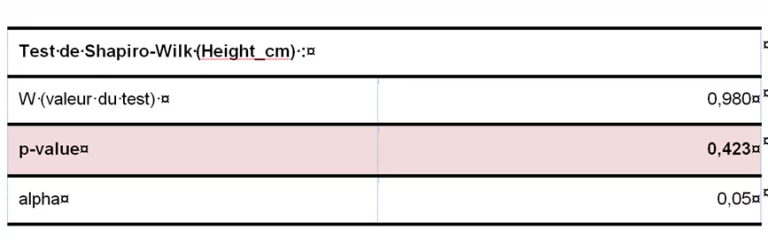
Ci-dessous le tableau des résultats d’un test de Shapiro-Wilk. W est la valeur du test et la p-value est égale à 0,423. Elle est inférieure à 0,05. Nous acceptons donc l’hypothèse nulle et nous concluons que la distribution de la variable « Height » suit une loi Normale.
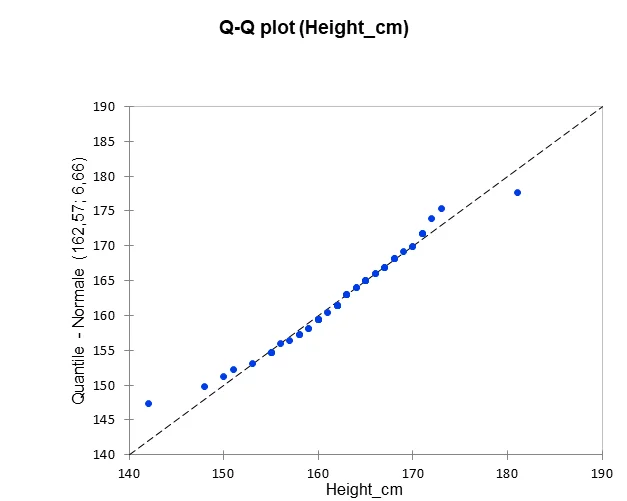
Le tracé Q-Q plot montre que les valeurs de la variable « Height » sont bien alignées sur la droite du graphique.
Par contre le test de Shapiro-Wilk appliqué à la variable Cytorachie (c/ul), donne une p-value < 0,0001. Les données de cette variable ne suivent pas une distribution normale.
Test de Normalité de Kolmogorov-Smirnov
Le test de normalité de Kolmogorov-Smirnov est équivalent au test de Shapiro-Wilk. Mais il est plus adapté aux grands échantillons taille ≥ 50.
Si cet article vous a été utile, Merci de le partager