METHODOLOGIE D'ANALYSE ET CHOIX DU TEST STATISTIQUE
Selon les objectifs de l’étude et de ses critères d’évaluation, l’analyse statistique doit s’adapter au plan expérimental. Selon si votre étude est comparative ou explicative et suivant si son critère est à échelle quantitative ou qualitative, la méthode d’analyse est différente. Le test statistique est aussi différent si les groupes à comparer sont en appariés, en indépendants ou en cross-over. De même, d’autres types de tests doivent être envisagés si l’analyse est en univariée ou en multivariée.
Sommaire
Petite précision
Les explications ci-dessous sont pour une compréhension globale et pour bien choisir le test statistique le plus adapté à vos données. Les détails de calcul et de réalisation de chaque test sont expliqués dans les autres articles de notre blog. Nous aborderons ici uniquement les tests statistiques de base pour des comparaisons ou des corrélations en univarié.
Qu'est-ce qu'est un test statistique ?
Un test statistique vérifie une hypothèse formulée sur les paramètres descriptifs (moyennes, pourcentages, variances, …) des séries à comparer.
Il vise en réalité à savoir si la différence observée entre les paramètres calculés dans l’échantillon (moyennes ou pourcentages) existe réellement dans la population.
Le principe d’un test statistique consiste à calculer une expression mathématique sur l’ensemble des données de l’échantillon. La valeur calculée est ensuite comparée à la distribution d’une loi théorique connue : Loi Z Normale, Loi T de Student, Loi de Fisher ou la loi du χ².
En pratique la valeur du test calculée est comparée à une valeur théorique de la table de la loi en question (d’où est tiré le test).
Par exemple pour le Test T de Student, sa valeur calculée t0 sera comparée à une valeur fixe t(α). Avec Alpha α est le risque d’erreur fixé à priori. Pour mieux comprendre le risque α (Alpha) voir l’article notre article de blog p Value et significativité d’un test« .

Comment choisir un test statistique ?
On choisit un test statistique selon plusieurs critères. Tout d’abord selon le type d’étude envisagée.
Etude Comparative ou Explicative
Premièrement on choisit un test selon le type de l’étude ou d’analyse à réaliser. Si l’étude est de type comparative. Par exemple pour comparer l’IMC entre deux groupes de traitements, le test à appliquer est un test de comparaison.
Si par contre l’objectif de l’étude est d’expliquer un facteur à partir d’un autre facteur, ou lors de la recherche d’une relation entre deux ou plusieurs paramètres. Par exemple pour une étude visant à chercher la relation entre la consommation du tabac et le cancer du poumon. Pour ce type d’analyse, il faut appliquer un test de corrélation.
Selon le type de variable à analyser – échelle quantitative ou qualitative
La nature du critère principal est très importante pour le type de test à appliquer.
Quand ce critère ou la variable est de type quantitatif, les tests à appliquer sont soit le test T de Student, ANOVA ou le test de Wilcoxon par exemple.
Si la variable à analyser est de type qualitative, tel que le taux de guérison ou le nombre d’amélioration. Dans ce cas la grandeur étudiée est la fréquence et le pourcentage et le test de Khi-deux est le plus adapté.
Normalité des données et égalité des variances
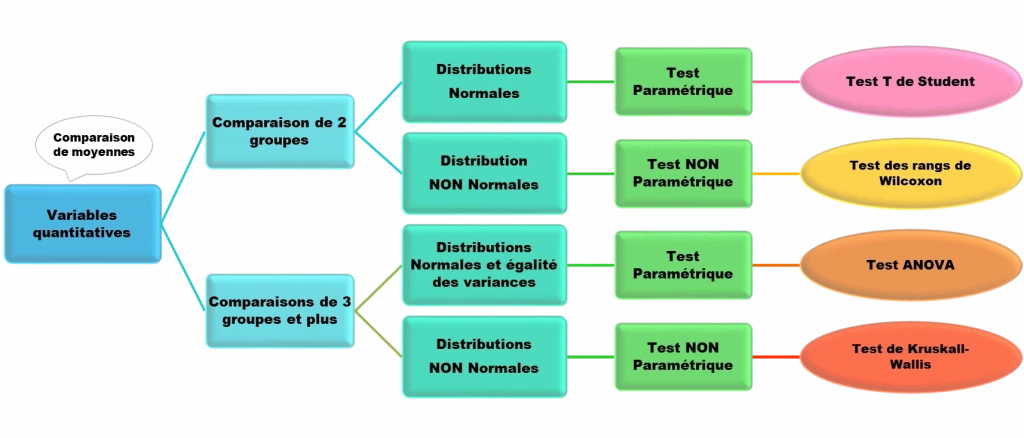
La troisième condition est la normalité de la distribution des échantillons étudiées et l’égalité de leurs variances. Pour les données qui suivent une loi normale, nous privilégions toujours les tests paramétriques. C’est à dire le test T de Student et l’ANOVA. Si cette condition n’est pas remplie, nous devons utiliser des tests non paramètriques tel que le test de Wilcoxon, test de Mann Whitney ou un Kruskal Wallis. Le schéma ci-dessous permettra de mieux comprendre dans quel cas utilisé chaque test.
Taille des échantillons
Enfin la taille de l’échantillon ou le Nombre total des sujets de l’ensemble des données N (N > 30 ou N ≤ 30) est un critère pour choisir le test statistique. Cette dernière condition s’applique uniquement aux tests de comparaison de deux moyennes. Dans les deux cas, N > 30 ou N ≤ 30, c’est le test T de Student qui doit être utilisé. La seule différence réside dans le choix de la table des nombres. Soit la table de la loi de Student ou celle de la loi Normale centrée réduite Z, pour comparer la valeur de t0 (Valeur du test T de Student). Je ne détaille pas cette dernière condition car elle est prise en considération lorsque nous utilisons un logiciel de statistique.
Test statistique de comparaison de variables quantitatives
Test T de Student pour comparer entre deux moyennes
Si vous cherchez à comparer un facteur quantitatif (variable quantitative) entre DEUX groupes de patients. Les grandeurs étudiées sont les moyennes (moyenne1 et moyenne2). Elles doivent êtres comparer entre les deux groupes par un test T de Student. Ce dernier permet de savoir si la différence observée entre les moyennes des deux échantillons est significative entre les deux groupes de populations. Le test T de Student est un test paramétrique. Cela veut dire que pour pouvoir l’appliquer, il faut que vos données suivent une distribution Normale. Si ce n’est pas le cas, il faut utiliser un test non paramétrique équivalent, tel que le test des rangs de Wilcoxon ou le test de Mann Whitney.
Il est à noter que deux types de test T de Student existent
Test T de Student pour données Indépendantes ET
Test T de Student pour données appariées
ANOVA pour la comparaison de 3 moyennes ou plus
Si l’étude vise à comparer entre plus de deux groupes (3 ou plus), c’est une analyse de variance ou ANOVA qui est à appliquer. A condition, comme dans le cas du test T, que les données des échantillons suivent une distribution Normale et d’égalité des variances. Dans le cas contraire, le test de Kruskal Wallis doit être appliqué.
Le résultat d’ANOVA donne une comparaison globale entre les trois groupes (ou plus). Des comparaisons entre les groupes deux à deux est possible grâce à des tests Ad-Hoc tel que les tests de Scheffé , test de Tukey, test de Bonferroni ou les contrastes orthogonaux. Par contre, dans le cas d’ANOVA, l’utilisation du test T de Student pour évaluer entre les groupes deux à deux, n’est pas appropriée et elle introduirait des erreurs.
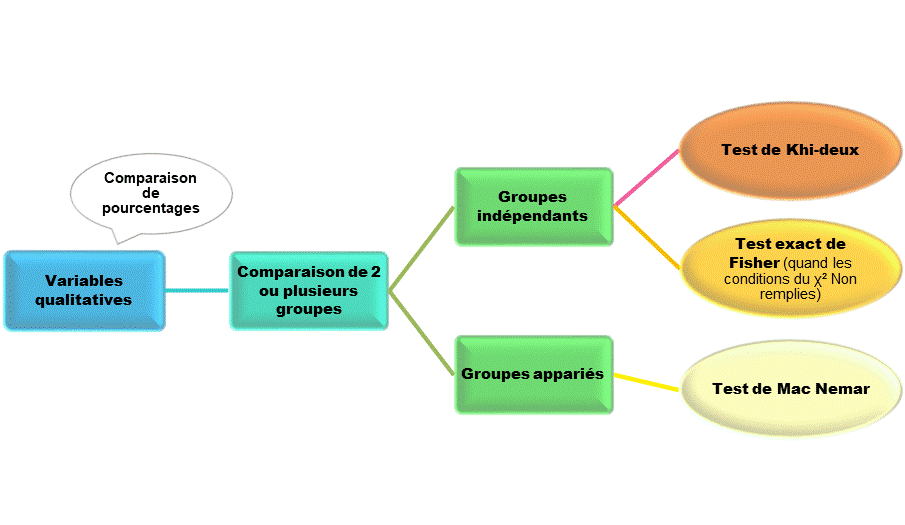
Test de Khi-deux
Si votre critère d’évaluation est un facteur qualitatif, comme par exemple la comparaison du pourcentage d’amélioration chez des groupes de patients. Le test de Khi-deux (Chi-2 ou χ² ) permet de comparer entre deux ou plusieurs séries de données (groupes de patients). Le test de Khi-deux obéit à une autre condition. Le nombre ou la fréquence des individus dans chaque classe de groupe ne doit pas être inférieur à 5. Si cette condition n’est pas remplie, il faut utiliser le test Exact de Fisher à sa place.
Le Khi-2 est un test non paramétrique. Pas de condition de normalité pour son application.
Analyse de corrélation et test du coefficient de corrélation
Pour les études dont l’objectif est d’évaluer la relation entre deux ou plusieurs facteurs. Par exemple la recherche des facteurs de risque d’une maladie. Comme dans le cas des tests de comparaison, les tests à choisir sont conditionnés par plusieurs facteurs. Le facteur primordial dans les tests de corrélation est la nature des variables étudiées.
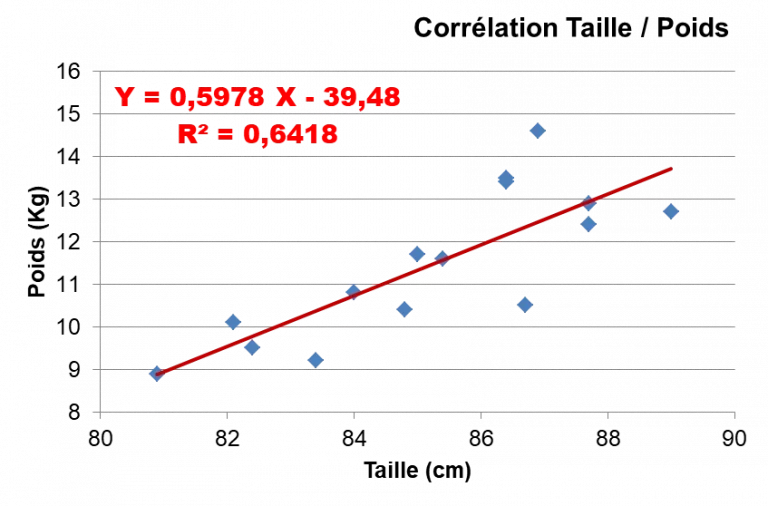
Premièrement cas ou les deux facteurs dont on veut déterminer la relation sont de type quantitatifs, le test à appliquer est un test de corrélation. Ce test est précédé par le calcul du coefficient de corrélation de Pearson R (ou R²). Dans ce dernier cas, il faut que les données suivent une distribution Normale. Sinon, c’est le coefficient de Spearman qui doit être calculer.
Deuxième cas lorsque l’on recherche l’existance d’une relation entre deux facteurs qualitatifs, donc entre fréquence ou pourcentage, nous devons utiliser un test de Khi-deux.
Et en troisième cas ou la recherche de corrélation est entre un facteur quantitatif et un facteur qualitatif. Nous devons appliquer une analyse de variance ANOVA.
Modèles d'analyse en multivariées
Pour tous ces cas mentionné jusqu’à présent, l’analyse est en univariée. C.-à-d. on recherche une comparaison ou une corrélation entre deux facteurs à chaque fois.
Le plus souvent et pour expliquer un phénomène, une caractéristique ou une pathologie, plusieurs facteurs interviennent. L’analyse doit être élaborée en multivariée en étudiant simultanément plusieurs facteurs de types quantitatif et qualitatif.
Dans le cas par exemple ou vous avez besoin de comparer entre un ou plusieurs critères en fonction du temps, un modèle linéaire à mesures répétées ou un modèle mixte est plus approprié pour les données longitudinales.
D’autre types d’analyse plus ou moins élaborés existent. Telle que la régression logistique, les modèles linéaires généralisés et mixtes dont il faut construire un modèle et l’ajuster aux données et aux facteurs étudiés.
Si cet article vous a été utile, Merci de le partager