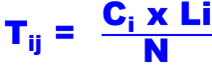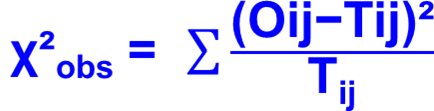TEST DE KHI-DEUX SUR EXCEL
Le test de Khi-deux est un test statistique non paramétrique s’applique aux données qualitatives. Il permet de comparer les effectifs de deux ou plusieurs séries de données qualitatives. Mais il mesure aussi la relation ou la liaison entre deux ou plusieurs groupes de variables qualitatives. Nous verrons dans cet article, comment réaliser le Test Khi-deux sur Excel directement avec la fonction « TEST.KHIDEUX ». Mais avant cela, nous devons faire quelques étapes de calculs préalables, car l’application l’exige. Ces étapes de calcul servent aussi à comprendre comment fonctionne cette fonction et les étapes pour déterminer la valeur du test à la main.
Sommaire
Test de Khi-deux cas géneral
Dans un premier temps, nous expliquerons ci-dessous un cas général de comparaison de plusieurs groupes avec les différentes étapes de calculs théoriques pour la réalisation du test. Ensuite, nous réaliserons à l’aide d’un exemple, le test de Khi-deux sur Excel.
Les Etapes de réalisation du test de Khi-deux
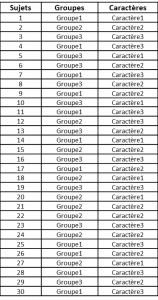
Nous voulons comparer plusieurs séries de données (dans le tableau de donnéees ci-dessous nous avons 3 groupes ) d’une même variable qualitative nominale à plusieurs classes (3 caractères 1, 2 et 3),
Tout d’abord nous posons les Hypothèses de l’étude:
– Hypothèse nulle H0: les pourcentages des 3 groupes sont égaux p1 = p2= p3. C’est à dire qu’il n’y a pas de différence entre les trois groupe. Versus
– Hypothèse alternative : H1 en bilatérale: les pourcentages des groupes sont différents p1 ≠ p2 ≠ p3. Il y a une différence significative entre les groupes comparer.
Nous fixons le risque d’erreur α = 5%.
1. Calcul du Tableau de contingence:
Calcul des effectifs Observés des caractères dans chaque groupe:
2. Calcul des effectifs Attendus ou Théoriques
A partir des données de l’échantillon, nous calculons les effectifs ou le nombre de chaque caractère dans chaque groupe.
Par exemple, le nombre de caractère1 dans le groupe1 = O11; le nombre de caractère1 dans le groupe2 = O21; …., etc. Ce qui nous donne le tableau de contigence ci-dessous.
Tableau de contingence à L Lignes et C Colonnes
O = pour valeur Observée ou fréquence calculée à partir des données réelles pour le groupe et le caractère donné.
Oij = O11, …O22, …O32 sont les effectifs observés dans l’échantillon.
O11 = Fréquence ou Nombre de carractère1 observé dans le groupe1; O12 = Nombre de carractère2 observé dans le groupe1; … etc.
Ci = Total colonne i ; Li = Total ligne i.
L = Ligne, c’est le total des valeurs observées dans une ligne. Dans cet exemple nous avons trois lignes L1, L2 et L3.
L1 = Total Ligne1 = total des effectifs du caractère1 dans l’échantillon.
C = Colonne, c’est le total de la colonne. Ici il y a 3 colonnes C1, C2 et C3.
C1 = Total colonne1 = total des effectifs des caractères dans le groupe1
Dans un autre tableau, nous allons calculer cette fois-ci, les effectifs théoriques ou les effectifs attendus Tij sous H0. Pour expliquer concrètement les effectifs, nous pouvons les considérer comme les effectifs idéaux rencontrés dans le cas où tous les groupes sont égaux entre eux. C’est à dire attendus sous l’hypothèse nulle H0.
Donc, pour chaque case du tableau nous devons calculer les valeurs Tij :
Valeur Théorique ou attendue
Tableau de contingence avec valeurs attendues
T11 = L1xC1/N ; T12= L1xC2/N ; T33 = L3xC3/N ; …
L1 =Total de la ligne1 , C1= total de la colonne1
Par exemple la Valeur théorique de la Case1 = Somme des valeurs de la colonne 1 (C1) X la somme des valeur de la ligne 1 (L1) divisée par le Nombre totale d’observation N.
3. Calcul de la valeur du test du Khi2:
Comme pour chaque test statistique, le test de Khi-deux a une une formule de calcul de saa valeur accompanée toujours de son propre degrés de liberté dll.
Test de Khi-deux, Avec dll= (L-1)(C-1)
dll= degrés de liberté = (L-1)(C-1) dans la table de la loi de χ²
∑ = somme ou addition des valeurs ou fréquences observées et théoriques.
Nous posons les hypothèses de l’étude:
Hypothèse nulle H0: p1 = p2= p3: Il n’y a pas de différence entre les groupes
Hypothèse alternative : H1 bilatérale: p1 ≠ p2 ≠ p3. Il y a une différence entre les groupes.
Risque d’erreur fixé à α = 5%
4. Comparaison de la valeur du test à la valeur seuil α dans la tables de χ²
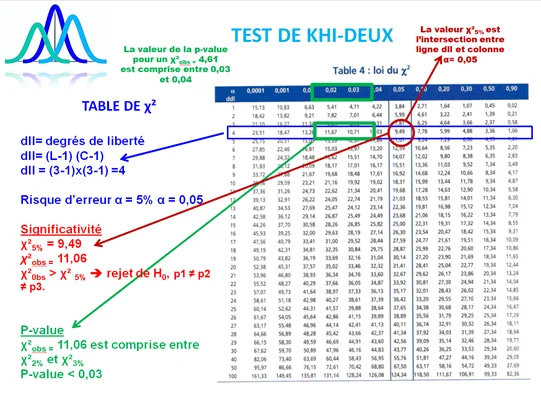
Une fois la valeur du Khi-deux χ² obs est calculée à partir des données de notre échantillon, nous devons la comparer à la valeur seuil α de 5% χ²(5%) (valeur du risque alpha fixée à 5 %) dans la table du Khi-deux.
Deux résultats sont possibles:
Soit : χ²obs < χ²(5%) cela signifie que l’on accepte H0, il n y a pas de différence entre les groupes comparés.
Soit : χ²obs ≥ χ²(5%) dans ce cas, on rejette H0, il y a une différence significative entre les groupes comparés.
Dernier point du test de Khi-deux calculé à la main. C’est la recherche de la valeur p ou p-value dans la table de Khi-deux.
5. Significativité du test ou p-value dans la table de Khi-deux
Il est possible de rechercher la p-value du test directement dans la table du Khi-deux (Voir explication dans l’exemple de la tables ci-dessus).
Une fois trouvée dans la table, il faut comparer sa valeur p à la valeur du risque alpha de 0,05. Comme dans le cas précedent, deux résultats sont possibles:
Soit p-value > 0,05, on accepte H0, il n y a pas de différence entre les groupes comparés.
Soit p-value ≤ 0,05, on rejette H0 et on conclut qu’il y a une différence significative entre les groupes comparés. Ou au moins un groupe est statistiquent différent des autres.
Pour savoir comment trouver la p-value dans la table, suivre les explications dans l’image ci-dessous.
Test de Khi-deux sur Excel
Pour mieux comprendre les étapes de réalisation du test du Khi-deux sur Excel nous présenterons les différentes étapes à l’aide d’un exemple de jeu de données.
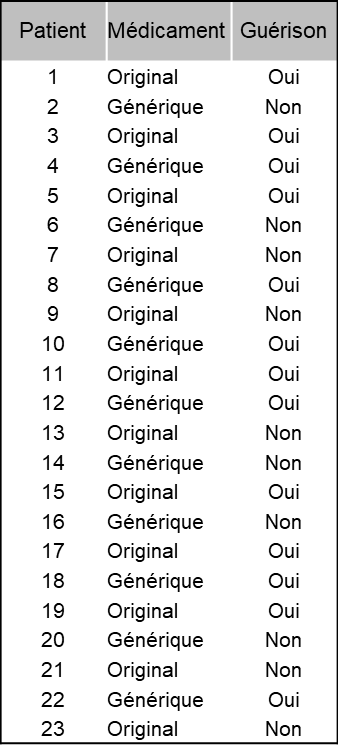
Nous voulons comparer les effets de deux médicaments dans la guérison des malades. Nous étudions donc la relation qui peut exister entre le type de médicament (Original et Générique) et le pourcentage de guérison des malades.
Les deux médicaments (Original et Générique) ont été administrés à deux groupes de patients. Nous observons les effectifs de patients guéris (Oui) et Non guéris pour chaque médicament administré.
Le test du χ² permet de comparer les pourcentages de guérison dans chaque groupe de malades. Et de savoir lequel des deux médicaments a guérit significativement plus de patients.
Fonction du Test de Khi-deux de MS Excel
La fonction de MS Excel pour réaliser le test de Khi-deux est:
=TEST.KHIDEUX(plage_réelle; plage_attendue)
En tapant la foction =TEST.KHIDEUX, il faut selectionner les cellules de la « plage_réelle » qui sont les valeurs observées et calculées dans une tables de contingence. Puis les cellules de la « plage_attendue » qui sont les valeurs théoriques calculées préalablement comme décrit ci-dessus. La fonction du test de Khi-deux va ensuite comparer les valeurs de la plage_réelle à ceux de la plage_attendue et donnera directement la significativité du test ou la p-value.
Donc pour utiliser la fonction TEST.KHIDEUX ou CHISQ.TEST en version anglaise dans notre exemple, deux étapes sont Obligatoires.
Première étape, calcul des valeurs observées ou les effectifs des données de l’échantillon pour chaque catégorie de « malade », guéris et non guéris dans chaque groupe de médicament, Original et Générique.
La deuxième étape consite à calculer des valeurs théoriques (formule de calcul des effectifs théoriques ci-dessous).
1. Calcul des effectifs Observés dans l'échantillon
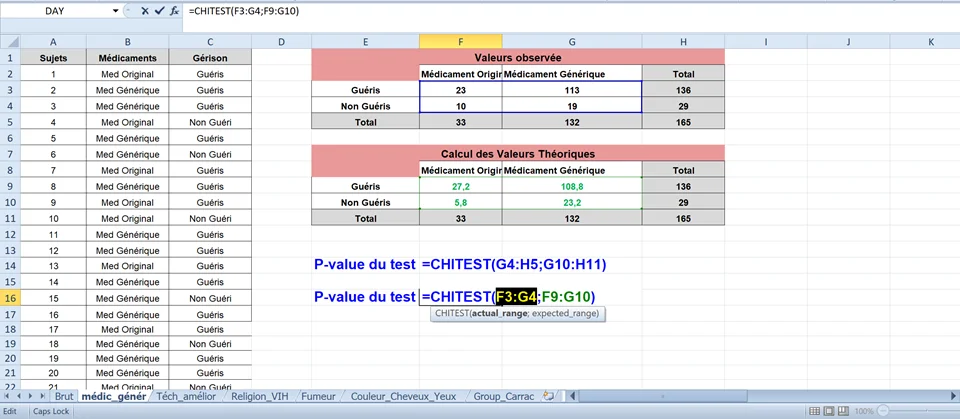
Tableaux de contingence à quatre cases des valeurs observées:
p1 = 70% et p2= 86% sont les pourcentages de guérison dans chaque groupe. Nous observons que p1 < p2 mais cette différence est elle significative ?
Hypothèses de l’étude: H0: p1 =p2 / H1 Bilatérale: p1 ≠ p2; (ou H1 unilatérale p1< p2 ou p1>p2);
2. Calcul des effectifs théoriques pour chaque case du tableau Tij = Ci x Li / N
3. Test de Khi-deux avec la fonction Excel "Test.Khideux" donne la p-value
Une fois les valeurs ou les effectifs observés et théoriques on été calculés, la fonction de Excel TEST.KHIDEUS vous demandera de sélectionner des plages réelle et attendue.
=TEST.KHIDEUX(plage_réelle; plage_attedue) ou
Dans notre exemple =TEST.KHIDEUX(G4:H5;G10:H11) » ou CHITEST(G4:H5;G10:H11) » va comparer les valeurs réelles aux valeurs attendues et donnera la valeur de 0,0317418 .
Cette valeur calculée de 0,0317418 est la p-value du test du Khi-deux.
La p-value est ensuite comparée au seuil du risque alpha fixé à priori à 5%.
La p-vaue de 0,0317418 est inférieure à 0,05. Nous rejetons H0. H1 est retenue: Il y a un différence statistiquement significative entre les deus médicaments.
4. Conclusion statistique de l’exemple:
En conclusion, le pourcentage de 86% de malades guéris dans groupe de médicament Générique (calculé à partir de notre échantillon) est statistiquement supérieure à celuis du groupe médicament Originale (70% de guérison) avec p-value = 0,032.
La fonction Test Khi-deux de MS Excel donne dirrectement la p-value.
Conditions d’application du test de Khi-deux
En résumé
Pour résumer tous ce qui a été dit jusqu’à présent, le Khi-deux s’applique aux données qualitatives. C’est un test non paramétrique. C’est à dire, qu’il n’y a pas de nécessité d’avoir une distribution normale des données pour l’appliquer.
Le test Khi-deux est un test généraliste, il a plusieurs utilités.
Tout d’abort, le test de Khi-deux de conformité ou d’ajustement. Ce test permet de comparer la distribution d’un échantillon à la distribution connue d’une population (de référence)
Par Exemple. Comparer le pourcentage des centenaires de la population Française au pourcentage des centenaires d’un village du Népal (population de référence connue pour sa longévité).
Deuxièmement, le test de Khi-2 d’Homogénéité. Il compare les effectifs de deux ou plusieurs échantillons d’une même variable qualitative nominale ou ordinale.
Ex. Comparaison du % de réussite des étudiants de l’université Lyon2 et ceux de l’université de Montpelier.
Test de Khi-2 de contingence. Comme dans l’exemple ci-dessus, c’est un test qui compare le pourcentage de deux échantillons d’une variable binaire, oui/non, malade/ pas malade ou 1 / 0.
Ex. Comparaison de pourcentages de guérison par deux traitements.
Enfin le test de Khi-2 de corrélation utilisé pour chercher une relation ou une liaison entre 2 ou plusieurs variables qualitatives.
Tous ces tests ont le même principe et présentent les mêmes étapes de calculs que celui présenté et expliqué ci-dessus.
Si cet article vous a été utile, Merci de le partager