Le Test de Wilcoxon est un test de comparaison de deux séries d’une même variable quantitative (même unité de mesure). C’est un Test non paramétrique, utilisé quand les conditions de normalité de la variable ne sont pas valides. C’est l’équivalent du test T de Student. Mais contrairement à ce dernier, le test de Wilcoxon compare les séries en comparant les rangs de leurs valeurs. Il en existe deux types: Test de Wilcoxon pour séries indépendantes et Test de Wilcoxon pour séries appariées.

Principe du test de Wilcoxon

Le test de Wilcoxon compare deux séries ou groupes de données d’une même variable quantitative ou semi-quantitative. Il s’applique lorsque nous ne pouvons pas utiliser le test T de Student car les conditions de normalité des données ne sont pas validées. Contrairement au test T de Student qui compare les données en comparant leurs moyennes, le test de Wilcoxon compare les rangs des valeurs des deux séries.

En effet le test de Wilcoxon range les valeurs des deux séries et leur attribut un RANG. Ensuite il compare la somme des rangs d’une des deux séries et la somme des rangs attendue sous H0.

Ceci veut dire que sous l’hypothèse nulle H0, l’alternance des valeurs des rangs des deux séries est régulière. Ou en d’autres termes, les rangs des valeurs des 2 séries doivent être mélangés d’une façon homogène sous H0.

En posant les hypothèses du test de Wilcoxon:

Hypothèse nulle H0 : Les deux distributions sont homogènes ou superposées, versus

Hypothèse alternative H1 bilatérale: Les deux distributions sont décalées. Ce qui revient à dire que les deux séries sont différentes.

Valeur du Test de Wilcoxon pour données indépendantes

Valeur du test en indépendant:

w₁ est la somme des rangs de la série la plus courte;

wa est la somme des rangs attendus sous H0 avec s²w1 est la variance de la série w1 qui est égale à

n1 et n2 sont les effectifs de la série1 et de la série2 respectivement et N = n1+n2 est la somme des effectifs des 2 séries.

Significativité du test de Wilcoxon

Comme pour tous les tests statistiques, une fois que nous avons calculé la valeur du test de Wilcoxon W0, nous devons comparer sa valeur à la valeur correspondante au risque alpha. Dans le cas de ce test,  cette valeur W0,05 est égale à 1,96 dans la table de la loi Normale centrée réduite Z.

Et comme à chaque fois deux résultats sont possibles:

Soit W0 < 1,96 et donc on accepte H0. Les deux séries sont Homogènes et donc les deux séries sont égales.

Soit W0 ≥ 1,96 nous devons donc rejeter H0, H1 est vraie. Les deux séries sont décalées ou différentes. Nous pouvons conclure que la moyenne serie1 m1 est ≠ moyenne m2 de la série2.

OU alors nous cherchons directement le degré de significativité du test ou  la p-value dans la table Z de la loi centrée réduite.

p-value > 0,05 ; nous acceptons H0 et les deux séries sont Homogènes ou elles sont égales.

p-value ≤ 0,05 ; nous rejetons H0. Les deux séries sont différentes ou les deux moyennes sont différentes m1 ≠ m2.

Un exemple pour comprendre

En effet pour mieux comprendre les étapes de calcul du test de Wilcoxon, quoi de mieux qu’un exemple d’application très simple.

Nous voulons comparer les scores d’amélioration entre deux groupes de patients traités et non traités. Les deux séries de données sont indépendants puisque les patients traités et non traités sont distincts.

En addition, le test de normalité réalisé nous indique que les scores d’amélioration ne suivent pas une distribution Gaussienne. De ce fait nous ne pouvons pas appliquer le test T de Student. Nous allons donc comparer entre les deux séries de données à l’aide du test de Wilcoxon pour données indépendantes.

Nous allons réaliser l’ensemble des calculs de ce test sur Excel.

Première étape, attribution des rangs aux valeurs

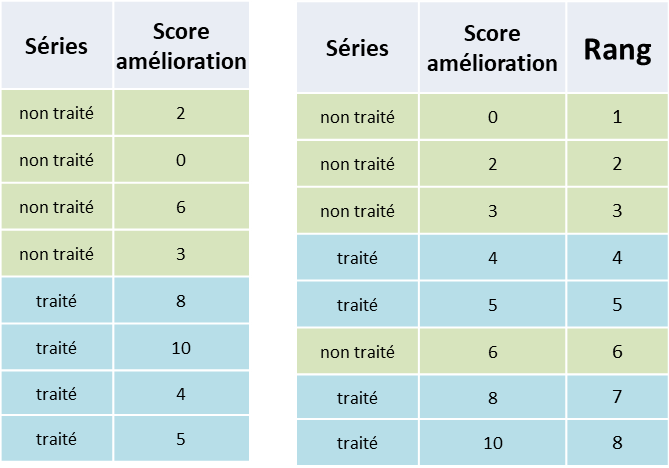
Premièrement nous devons trier par ordre croissant la variable scores d’amélioration des deux séries mélangées.

Ensuite dans une autre colonne, nous attribuons un rang à chaque valeur des séries comme montré dans le tableau ci-dessous. Pour les valeurs identiques, nous attribuons des rangs ex-aequo en calculant la moyenne des rangs qu’elles occupent. Ou sous MS Excel appliquer la fonction « Rang.moyen » ou « moyenne.rang » selon la version de l’application.

Deuxième étape, calculs de la somme des rangs de l’une des deux séries.

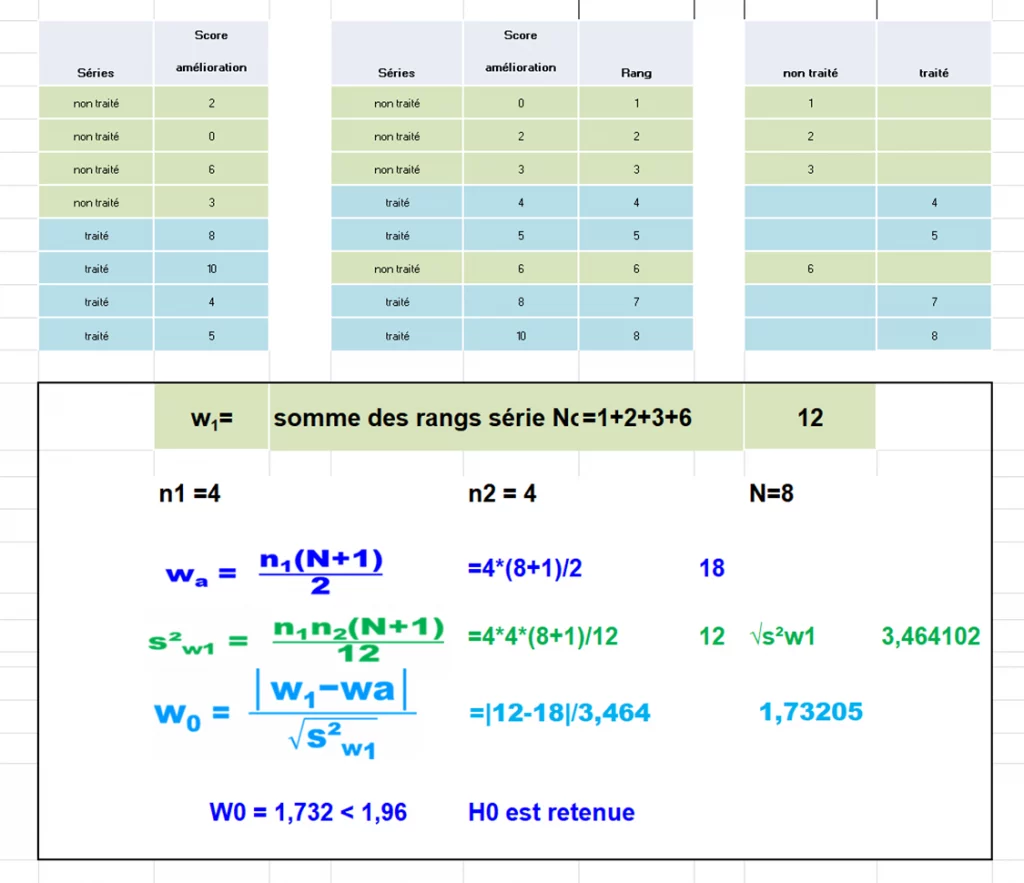
Deuxièmement, nous devons calculer la somme des rangs w1 de la série la plus courte. Ou prendre la valeur la plus faible. Ensuite nous passons aux calculs ci-dessous:

3° Calcul de la somme attendue wa = n1(N+1)/2

4° Calcul de la variance s² de w1 suivant la formule sw1= n1n2(N+1)/12

5° Enfin nous calculons la valeur du test w0 puis la comparer à la valeur de 1,96 (Valeur Z pour un α=5%)

Ces différentes étapes ont été réalisées sur Excel.

En conclusion des résultats de cet exemple, W0 est < 1,96 ; il n’y a donc pas de différence d’amélioration entre les groupes traités et non traité.