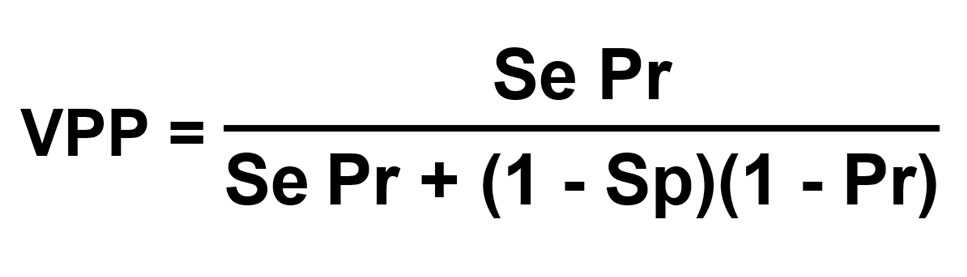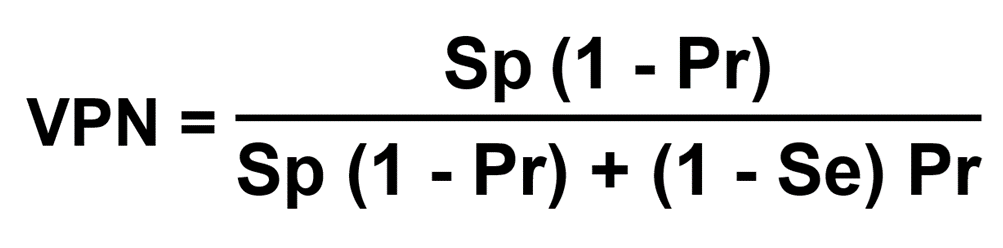Performance d’un test de diagnostique
Sensibilité, Spécificité, Courbe de Roc
Sommaire
L’analyse de performance d’un test de diagnostique regroupe un ensemble de méthodes statistiques permettant d’évaluer l’efficacité, la précision et la fiabilité des tests médicaux utilisés pour diagnostiquer des maladies ou des conditions de santé. L’objectif de l’analyse de performance est ainsi d’améliorer la qualité des diagnostiques, de minimiser les erreurs et d’optimiser l’utilisation des outils nécessaires dans la prise de décision médicale. Ces méthodes englobent les analyses de la sensibilité, la spécificité, les valeurs prédictives positives et négatives, ainsi que d’autres mesures de performance spécifiques aux tests. Nous détaillerons dans cet article, les principes de base des tests de diagnostique et les méthodes de leurs analyses. Nous utiliserons principalement le terme de Test pour définir n’importe quelle technique ou méthode de diagnostique biologique ou clinique.
Principe de l’analyse de performance d’un test de diagnostique
En médecine, les maladies sont reconnues grâce à des signes cliniques (fièvre, douleurs, gonflement…etc.) qui sont quelques fois combinés avec d’autres techniques paracliniques comme les examens biologiques ou l’imagerie. Ces différentes techniques que nous appellerons ici tests de diagnostique, qu’elles soient utilisées seules ou combinées, permettent de classer de manière sûre les malades des non-malades. En effet elles doivent être performantes de manière à écarter les faux positifs et les faux négatifs. Avant de pouvoir les appliquer à toute la population, nous devons appliquer des analyses statistiques de performances pour évaluer leur reproductivité, leur sensibilité et leur spécificité.
De point de vue statistique, le résultat d’un test de diagnostique peut être :
Soit une variable qualitative binaire dans le cas où le test donne uniquement deux résultats, positif ou négatif.
Soit une variable quantitative lorsque le résultat est une valeur d’un examen biologique ou d’une échographie. Les résultats du test ont une unité de mesure, par exemple mmoml/ml ou mg/l.
Mesures de performance d’un test de diagnostique
Un test de diagnostique doit obéir à deux qualités majeures, une sensibilité et une spécificité.
Sensibilité Se
La sensibilité notée se mesure la capacité d’un test à identifier correctement les cas positifs ou les malades. Pour mesurer la sensibilité d’un test de diagnostique, nous devons évidement avoir un groupe de vrais positifs VP (malades). Ce groupe doit être confirmé préalablement par une méthode de référence ayant fait preuve de sa valeur diagnostique. Ce sont donc des cas confirmés avec certitude.
L’application du test de diagnostique à évaluer à ces cas malades confirmés, donne deux résultats. Soit le résultat est positif, ce qui veut dire que le test détecte les vrais positifs (VP). Soit le résultat est négatif et donc le test a détecté des Faux Négatifs FN.
Tableau de contingence
Faux Positifs (Test + et pas de maladie) ou Faux Négatifs (Test – et maladie).
De point de vue statistique, la sensibilité d’un test est la proportion des Vrais Positifs VP sur le nombre total de cas (Malade M+). Evidement les cas sont les Vrais Positifs VP et les Faux Négatifs FN donnés par le test étudié.
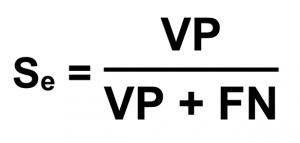
La sensibilité est une valeur comprise entre 0 et 1 et elle est exprimée en général en pourcentage.
Spécificité Sp d’un test de diagnostique :
La spécificité quant à elle évalue la capacité d’un test à identifier correctement les cas négatifs ou les non malades. De la même manière que pour la sensibilité, pour évaluer la spécificité d’un test de diagnostique, il faut disposer d’un ensemble de sujets sains. Ce groupe de sujets sains doit être confirmé préalablement par d’autres méthodes de diagnostiques de référence qui certifient de l’absence de la maladie pour ce groupe de sujet.
Si nous appliquons le test à évaluer à ce groupe de sujets sains, nous obtenons deux résultats. Soit le résultat est Négatif, le test a détecté un Vrai Négatif VN (sujet sain). Soit le résultat est Positif, le test a détecté un Faux Positif FP. La spécificité est donc définie comme la proportion des Vrais Négatifs sur l’ensemble des sujets sains (Non malades M-) ou (VN + FP).
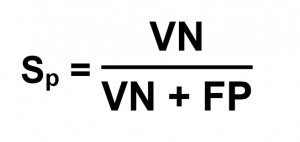La spécificité est une valeur comprise entre 0 et 1. On l’exprime en général en pourcentage.
Valeur Prédictive Positive VPP
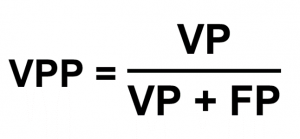
La Valeur Prédictive Positive notée VPP indique la probabilité qu’un cas identifié comme positif soit réellement positif VP. Autrement dit, c’est la probabilité d’être malade sachant que le résultat est positif.
La Valeur Prédictive Positive (VPP) est estimée par la proportion de vrais positifs ou malades parmi les sujets testés positivement.
Valeur Prédictive Négative VPN
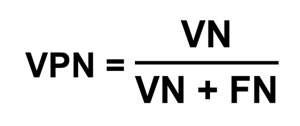
De la même manière, la Valeur Prédictive Négative VPN indique la probabilité qu’un cas identifié comme négatif soit réellement négatif. C’est à dire la probabilité d’être sain sachant que le résultat est négatif. Elle est estimée par la proportion des vrais négatifs (non malade) parmi les sujets testés négatifs.
La sensibilité, la spécificité, les VPP et VPN sont des mesures souvent utilisées pour évaluer la performance globale d’un test diagnostique.
La sensibilité et la spécificité sont deux caractéristiques propres au test lui-même. Ces valeurs aident à comprendre l’utilité clinique d’un test dans un contexte donné. Mais si nous ne connaissons pas, par une méthode de référence valide, les vrais positifs et les vrais négatifs dans l’échantillon. Et si nous devons appliquer ce test à une population déterminée, des caractéristiques propres à cette dernière doivent aussi être appliquées. C’est le cas où la prévalence de la maladie recherchée est plus élevée que dans la population générale.
Pour rappel, la prévalence d’une maladie est la proportion du nombre de malades observés à un temps t sur l’ensemble de la population dont sont issus les malades. Par exemple la prévalence de la toxoplasmose chez la femmes enceinte en France en un mois est de 42%.
Facteurs Influants sur la Performance d’un test de diagnostique
A ces effets, les valeurs de calcul des valeurs prédictives positives et négatives sont formulées à l’aide du théorème de Bayes dont les formules ci-dessous :
Valeur Prédictive Positive VPP et prévalence :
Valeur Prédictive Négative VPN et prévalence :
Se est la sensibilité, Sp est la spécificité et Pr est la prévalence de la maladie.
Ainsi les VPP et VPN d’un test dépendent de la prévalence de la maladie. Un test appliqué en situation de dépistage dans la population générale (Prévalence faible), aura un faible VPP et une forte VPN. De nombreux sujets seront testés positifs alors qu’ils ne sont pas malades. A l’inverse un test appliqué dans un service spécialisé (Prévalence élevée) aura une VPP élevée et un VPN faible. Dans les deux cas, la sensibilité et la spécificité ne varieront pas.
Valeurs prédictives et sensibilité et spécificité
- Plus la spécificité est élevée et plus le VPP est levée. En effet, la valeur (1 – Sp) est au dénominateur du VPP.
- La VPN dépend de la sensibilité car (1 – Se) est au dénominateur. Donc plus la sensibilité est élevée et plus la VPN est élevée.
On peut calculer d’autre paramètres tel que:
Indice de Younden J
J = Se + Sp – 1.
L’indice de Younden J varie de – 1 à + 1. Si J= 1, le test est parfait. Par contre s’il vaut 0, le test n’a aucune valeur diagnostique.
Rapport de vraisemblance RV ou LR (likelihood ratio en anglais)
C’est le rapport entre la fréquence du signe chez les malades et la fréquence du signe chez les non-malades. Ou encore le rapport de probabilité conditionnelle du signe chez les malades sur la probabilité
conditionnelle du signe chez les non-malades.
Rapport de vraisemblance positif “L” (likelihood ratio)
L = Se / (1 – Sp)
Idéalement infini, il est égal à 1 quand le test n’apporte aucune information.
Les rapports de vraisemblance permettent d’évaluer à quel point la probabilité d’un résultat positif ou négatif change en fonction du résultat du test. Ils offrent des informations sur la force de la relation entre le résultat du test et la présence ou l’absence de la maladie.
Performance d’un test de diagnostique quantitatif
Nous avons déjà mentionné plus haut, qu’un test de diagnostique peut être d’ordre qualitatif lorsque les résultats sont binaires de type présence / absence ou positif / négatif. Mais il peut être de type quantitatif caractérisé par des résultats numériques continues. Ces résultats sont différents d’un sujet à un autre exprimés en unité de mesure. C’est le cas de la majorité des tests biologiques exprimés en unité.
Dans le cas de ces tests quantitatifs, il faut définir une valeur seuil qui permettra de classer les positifs ou malades des négatifs ou non malades. Le choix de cette valeur seuil influencera la sensibilité et la spécificité du test et donc ses valeurs prédictives. Il est tout à fait possible de choisir une valeur seuil permettant d’obtenir une sensibilité et une spécificité égaux à 100%. Malheureusement cette situation est rarement possible en biologie médicale. Tout choix de valeur seuil conduira dès lors à des erreurs de classifications. Certains sujets malades (M+) seront classés négatifs (-), d’autres seront considérés comme positifs (+) alors qu’ils ne sont pas malades (M-). Voir le tableau de contingence ci-dessus.
Le plus souvent, il y a un chevauchement des deux distributions. Certains sujets sains peuvent présenter des valeurs positives (+). Et à l’inverse, des sujets malades peuvent présenter des valeurs identifiées comme négatifs (-). Le choix du seuil devient donc délicat car il divise les deux groupes en quatre groupes, VP, FN, VN et FP.
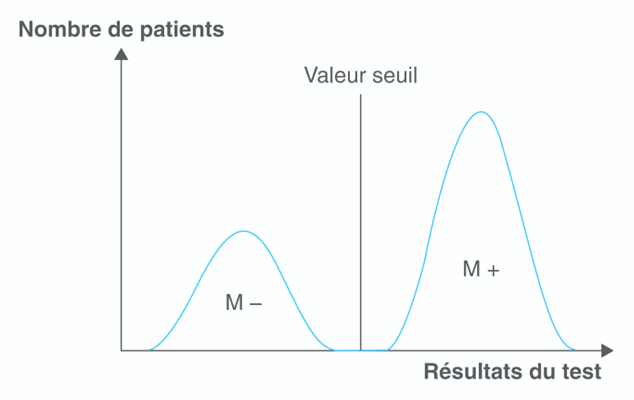
Cas d’un test Parfait où une valeur seuil sépare distinctement les distributions des groupes malade (M+) des non malade (M-).
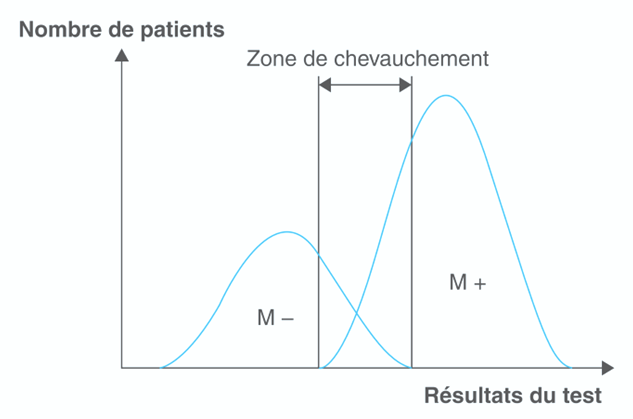
Condition réel d’un test quantitatif. Les résultats du test pour les sujets malades (M+) et non malades (M-) présentent un chevauchement. Certains sujets sains (M-) peuvent être considérés comme positifs (+) et des malade (M+) comme négatifs (-).
Choix de la valeur seuil
Toute tentative de changement du seuil aura des conséquences sur la qualité diagnostique du test et donc sur sa sensibilité et sa spécificité. Une diminution du seuil entraînera une diminution du nombre de faux négatifs d’où une augmentation de la sensibilité. Mais aussi une augmentation du nombre de faux positifs, donc une diminution de la spécificité. Inversement, une augmentation du seuil sera accompagnée d’une diminution des faux positifs et donc augmentation de la spécificité. Et d’une augmentation des faux négatifs et une diminution de la sensibilité. Ainsi, la sensibilité et spécificité varient inversement.
Chaque valeur de seuil est associée à des taux spécifiques de sensibilité et de spécificité, qui sont uniques à ce seuil particulier et ne caractérisent en aucune manière les performances du test pour d’autres valeurs de seuil. Cet aspect doit être pris en considération lors de la comparaison des tests diagnostiques et constitue l’une des informations clés de la courbe ROC.
Courbe ROC (Receiver Operating Characteristic)
La courbe ROC est un outil essentiel pour évaluer les performances diagnostiques des tests de laboratoire. Elle représente graphiquement la relation entre la sensibilité (ou probabilité de détecter un vrai positif) et la spécificité (probabilité de détecter un vrai négatif) d’un test, calculée pour toutes les valeurs seuils possibles. La courbe de Roc aide à visualiser la performance globale d’un test et à choisir le seuil optimal. L’axe des x représente le taux de faux positifs ou (1 – spécificité). L’axe des y représente le taux de vrais positifs ou la sensibilité. La ligne diagonale (ligne de référence) représente un modèle aléatoire qui n’a aucune capacité de discrimination.
Construction de la courbe de Roc
Pour construire la courbe de Roc, nous devons tout d’abord, classer les résultats du test par ordre croissant. Puis construire pour chaque valeur, un tableau de contingence comme le tableau décrit ci-dessus. Ensuite, nous devons calculer les effectifs VP, FP, VN et FN, ce qui permet de calculer la sensibilité et 1- spécificité du test pour chaque valeur seuil. Nous placerons ensuite chaque paire de valeurs (taux de faux positifs, taux de vrais positifs) sur le graphique. En reliant les points dans l’ordre croissant des seuils, cela donnera une courbe tracée en marches d’escaliers. La courbe reliera le coin inférieur gauche du graphique Se = 0 et Sp = 1 au coin supérieur droit Se = 1 et Sp = 0. C’est la courbe de Roc.
En continuité de cette démarche, nous ajoutons une la ligne de référence. C’est une ligne diagonale de (0,0) à (1,1) qui représente la performance d’un modèle aléatoire.
En effet, construire une courbe de Roc à la main est fastidieux. Les logiciels de statistiques permettent de réaliser le processus de calcul et de traçage de la courbe ROC.
Interprétation de la courbe de Roc
Lorsqu’on évalue la capacité discriminante d’un test, la courbe ROC représente la sensibilité du test (proportion de vrais positifs) par rapport à la spécificité (proportion de vrais négatifs) à différents seuils de coupure. Idéalement, nous voudrions que la courbe ROC soit le plus près possible du coin supérieur gauche, ce qui indiquerait une sensibilité élevée et une spécificité élevée.
Donc l’analyse de la courbe ROC pour évaluer la capacité de discrimination du test se fait par comparaison à la ligne de référence. Plus la courbe est éloignée de la ligne de référence vers le coin supérieur gauche (Se =100% et Sp= 100%), meilleure est la performance du modèle.
En utilisant la courbe de Rock, nous serons en mesure d’évaluer visuellement la performance du modèle de classification à différents seuils. Mais aussi de prendre des décisions éclairées sur la sélection du seuil optimal en fonction des besoins spécifiques du test et de la population.
La courbe ROC nous aide à avoir des compromis et à choisir le seuil qui convient le mieux aux besoins spécifiques du test en fonction de la population ciblée.
Si par exemple lors du développement d’un test médical pour détecter une maladie, nous souhaiterons minimiser les faux positifs (personnes en bonne santé inutilement traités contre la malade), nous pouvons choisir un seuil où la spécificité est élevée. Si nous voulons être très certain de détecter la maladie, nous devons choisir un seuil avec une sensibilité élevée.
Calcul de l’Aire sous la courbe (AUC) pour la performance d’un test de diagnostique
L’Air sous la Courbe est la mesure de l’espace sous la courbe de ROC. Cela peut être fait numériquement en intégrant la courbe ou approximativement en utilisant des méthodes telles que la règle du trapèze. Cette mesure quantifie la performance globale du modèle. Une AUC de 1.0 indique une performance parfaite. Tandis qu’une AUC de 0.5 est non-informatif et indique une performance équivalente à celle d’un modèle aléatoire. Par exemple:
- AUC de 0.9 ou plus : Suggère une excellente capacité discriminante. Le test est très performant et peut être considéré comme fiable pour la prise de décision.
- AUC entre 0.7 et 0.9 : Indique une capacité discriminante acceptable. Le test peut être considéré comme utile, mais il peut y avoir des améliorations possibles.
- AUC entre 0.5 et 0.7 : Montre une faible capacité discriminante. Le test peut ne pas être très utile dans la pratique clinique.
- AUC de 0.5 : Indique une performance équivalente au hasard. Le test ne présente pas de capacité discriminante.
Remarques importantes
Nous devons garder à l’esprit que l’interprétation de l’AUC dépend du contexte spécifique de l’étude et des objectifs cliniques. A cet effet nous devons considérer d’autres mesures de performance du modèle en conjonction avec l’AUC pour obtenir une évaluation plus complète.
Dans les prochains articles, nous développerons l’utilisation des courbes ROC pour comparer plusieurs tests diagnostiques et la reproductibilité et la concordance avec calcul des coefficients de concordance et Kappa.