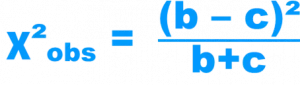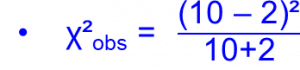Test de McNemar
Le test de McNemar, comme son équivalent le test de Khi-deux est un test statistique non paramétrique qui s’applique aux données qualitatives. Mais contrairement au test de Khi-deux, le test McNemar s’applique pour comparer entre deux séries de données appariées. Pour rappel les séries appariées sont des séries dont les mesures sont réalisées en intra-individuelle c’est-à-dire chez le même sujet. Comme par exemple pour évaluer des séries mesurées en avant après un traitement ou sur le côté droit et côté gauche d’un même individu ou lors d’un plan croisé (Cross over).
Sommaire
Réalisation du test de McNemar
Pour mieux comprendre le principe du test de McNemar, quand et comment l’appliquer pour comparer des séries de données, nous commençons par le présenter à l’aide d’un exemple simple.
Exemple
Nous voulons comparer les performances de deux techniques biologiques dans le diagnostique d’une maladie. Un total de 56 malades ont testé simultanément les deux techniques.
La performance ou sensibilité d’une technique est jugée par le nombre de résultats positifs enregistrés.
Nous voulons comparer les performances analytiques entre les deux techniques. ELISA est elle plus performante que IHAT ?
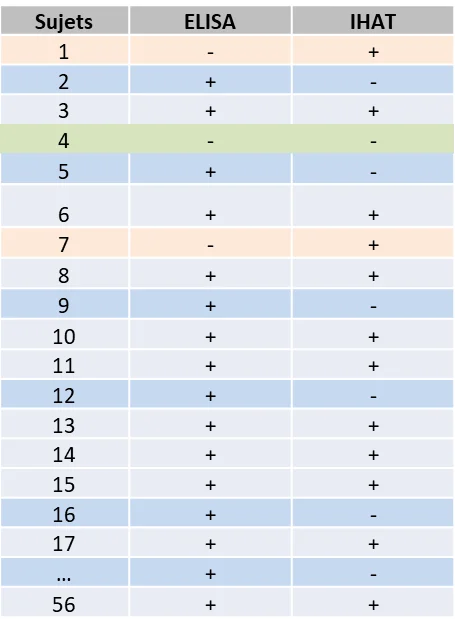
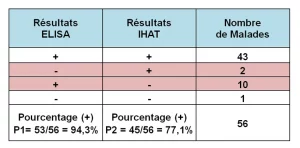
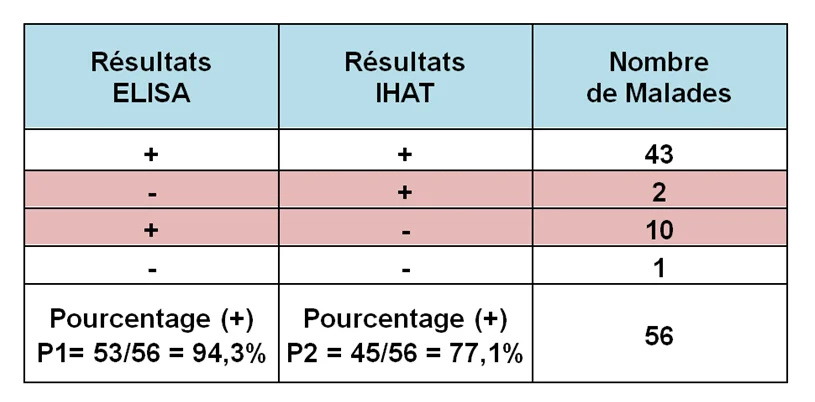
Les résultats du tableau ci-dessous montrent que pour certains sujets les deux techniques donnent des résultats concordants soit positifs (cas des sujets 3, 6, 8, …) ou négatifs (cas du sujet 4). Et dans d’autres cas les résultats des deux techniques ne sont pas concordants (c’est le cas des sujets 1, 2,5,…).
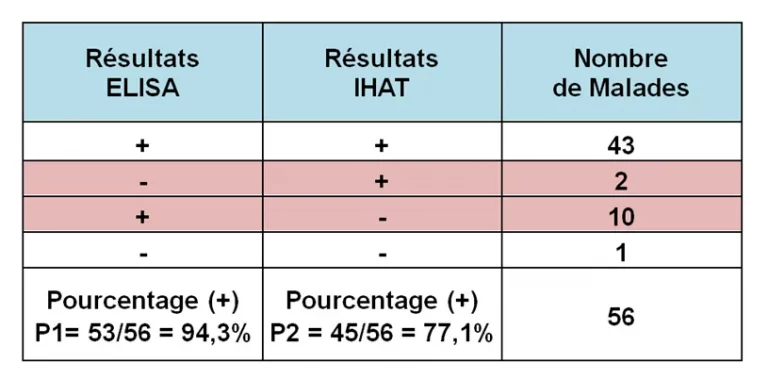
Dans un premier temps, nous calculons les fréquences ou nombres de paires concordantes dans chaque cas. Les 2 techniques donnent des résultats positifs pour 43 sujets et un résultat négatif pour un sujet. Quant aux paires discordantes ou les 2 techniques donnent des résultats différents, nous observons dans le tableau des fréquences, ces résultats chez 2 et 10 sujets respectivement
L’ELISA a rendu des positifs dans 53 cas sur 56 avec un pourcentage de p1=94,3%.
L’IHAT a rendu des positifs dans 45 cas sur 56 avec un pourcentage de p2=77,1%.
Nous devions donc comparer entre les deux techniques, en comparant les pourcentages des vrais positifs entre ELISA et IHAT.
Principe du test de McNemar
Le test de McNemar est un test statistique utilisé pour comparer entre des séries de données qualitatives. C’est à dire pour comparer des fréquences ou des pourcentages. Mais contrairement au test du Khi-deux, le test de McNemar a deux particularités. Premièrement, nous pouvons l’utiliser uniquement pour comparer entre deux séries de données. Deuxièmement, les données des séries doivent être en appariées et binaires (Oui/ Non).
Cela veut dire que pour un même sujet, nous devons avoir une valeur dans chaque série à comparer et cette valeur doit être dichotomique.
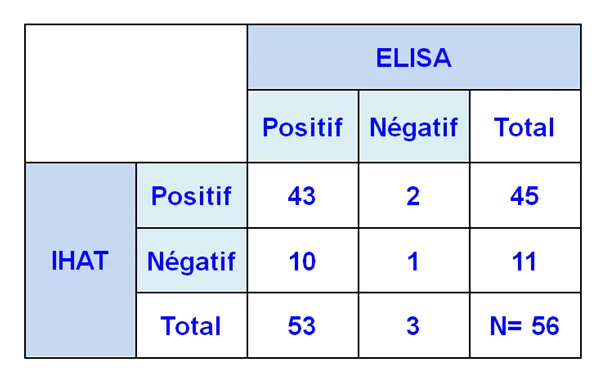
En premier lieu, nous devons représenter dans un tableau de données les fréquences enregistrées pour chaque série de données.
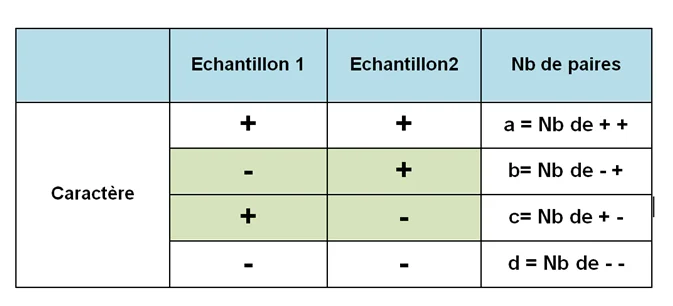
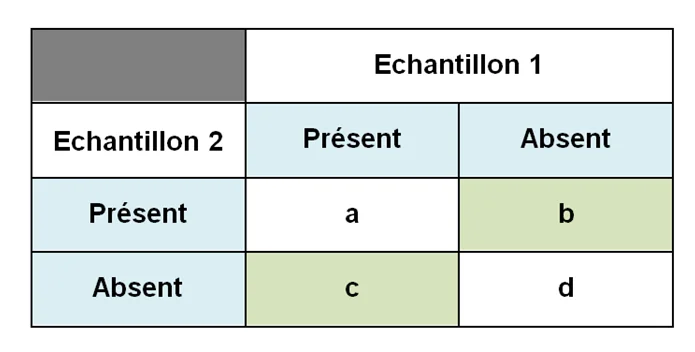
Les deux présentations sont équivalentes avec:
a et d est le nombre de paires concordantes.
c et b est nombre de paires discordantes ou opposés pour les 2 échantillons.
En outre, nous calculons les pourcentages de présence ou de vrais positifs dans chaque série. En effet dans l’échantillon1 le pourcentage (+) p1 = a+c / N.
Et dans l’échantillon2, le pourcentage (+) p2 = a+b / N.
Valeur du test de McNemar
La valeur du test de McNemar portera sur les seules paires discordantes b et c.
avec dll = 1
Comme pour chaque test statistique, sa valeur est accompagnée d’un degré de liberté (dll). Ce dll est généralement relié à la taille de l’échantillon et au nombre de comparaison. Dans le cas du test de McNemar, le dll est égale à 1 car il n’y a que deux séries ou groupes à comparer et que les données sont binaires.
Tout d’abord nous devons poser les hypothèses de l’étude pour expliquer ce que nous cherchons à démontrer.
Hypothèse nulle H0, les pourcentages des deux séries ne sont pas significativement différents p1 = p2. Versus l’hypothèse alternative H1 en bilatérale. L’un des deux pourcentages est supérieur significativement à l’autre.
Nous fixons aussi le risque d’erreur alpha α à 5%.
Une fois que nous avons calculé la valeur du test de McNemar, nous devons comparer sa valeur dans la table de la loi de Khi-deux ou χ².
Ensuite, les différentes étapes de recherche de la significativité du test de McNemar sont exactement les mêmes que celles utilisées pour le test de Khi-deux.
Significativité du test de McNemar
Premièrment, comparaison de la valeur du test χ²obs de McNemar à la valeur théorique dans la table de χ²(5%). Deux résultats sont possibles:
Soit χ²obs < χ²(5%) et donc nous acceptons H0 et nous concluons qu’il n y a pas de différence significative entre les deux pourcentages.
Soit χ²obs ≥ χ²(5%), nous rejetons H0, H1 est vraie. Et dans ce cas là, il y a une différence significative entre les pourcentages des deux séries.
Mais nous pouvons aussi chercher directement la p-value du test. Et cette fois-ci la p-value sera comparer au risque d’erreur alpha, 0,05.
Application avec l’exemple précédent
Pour l’application, nous utilisons l’exemple décrit plus haut pour réaliser le test de McNemar sur Excel.
Pour comparer la performance entre deux techniques biologiques dans le diagnostic d’une maladie, 56 malades ont testé simultanément les deux techniques.
L’ELISA a été rendu positive dans 53 cas sur 56 (94,3%) et IHAT a été rendu positif dans 45 cas sur 56 (77,1%).
Les paires discordantes sont plus utiles pour comparer entre les deux techniques. En effet, nous comptons le nombre de discordance pour calculer la valeur du test de McNemar.
χ²obs = 64/12 = 5,33 avec dll=1
Et comme expliquer plus haut, χ²obs est comparée à χ²5%.
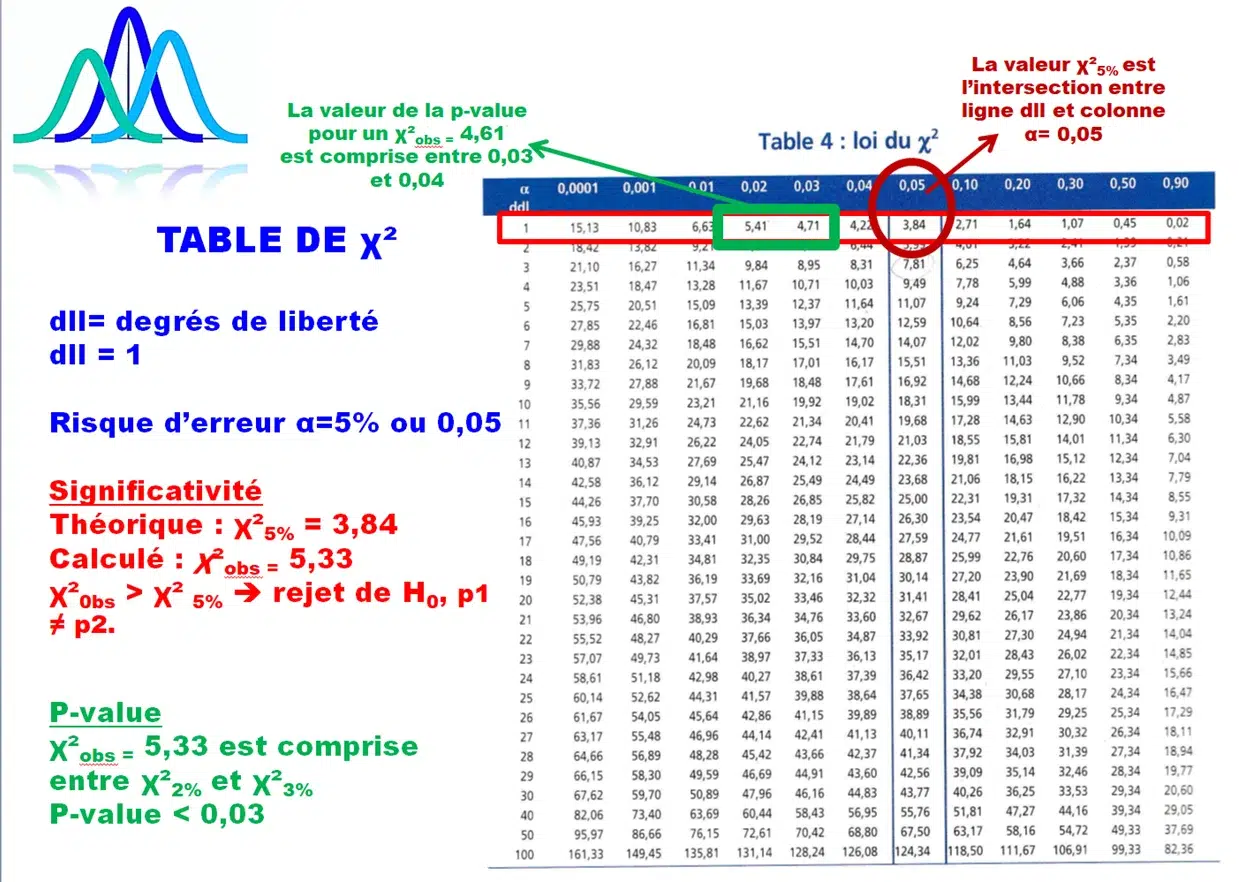
χ²obs est supérieure à χ²5% = 3, 84. On rejette donc H0 et / ou on cherche la p-value dans la table du Khi-deux.
Recherche de la p-value dans la table du Khi-deux
Sur la ligne de dll = 1 de la table, nous cherchons la valeur la plus proche et inférieure à la valeur du χ²obs (5,33). Cette valeur est égale à 4,71 et elle correspond à la valeur de significativité du test (c’est la ligne α juste au-dessus). La p-value dans ce cas-là est inférieure à 0,03.
La p-value est inférieur au risque alpha de 0,05.
En conclusion
Nous acceptons l’hypothèse alternative H0. Et nous pouvons conclure que les performances des deux techniques sont significativement différentes avec une p-value < 0,03.
Plus précisément, la technique ELISA est statistiquement plus performante pour le diagnostic de la maladie (p1>p2).
Si cet article vous a été utile, Merci de le partager