LES TESTS D'HYPOTHÈSE
Les tests d’hypothèse, sont des hypothèses statistiques formulées sur les paramètres descriptifs dont un test statistique doit vérifier. Un test d’hypothèse est donc une démarche en statistique Inférentielle qui permet de vérifier la validité de la question posée à l’ensemble de la population. Généralement lors d’une étude nous posons deux hypothèses, nulle H0 et son alternative H1. Les résultats du test permettent soit d’accepter, soit de rejeter l’hypothèse nulle posée. Ceci afin de prendre une décision claire sur les conclusions du test statistique et donc sur l’étude.
Sommaire
Principe des tests d'hypothèse
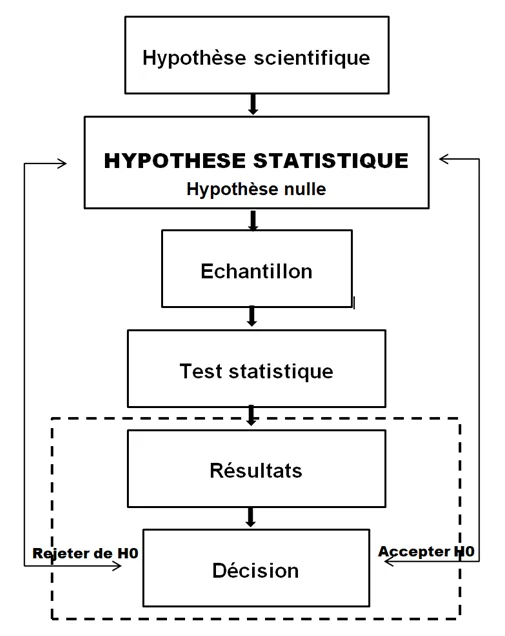
Lorsque nous avons une hypothèse scientifique à verifier, nous transformons cette question scientifique en une hypothèse statistique que nous devons vérifier avec un test statistique.
PROBLEMATIQUE
HYPOTHESE
TEST
Par exemple, nous voulons savoir si la durée moyenne de séjour en réanimation après une chirurgie abdominale µ1 est supérieure à la durée moyenne de séjour suite à une chirurgie vasculaire µ2 ? Nous voulons vérifier cette hypoyhèse avec un test statistique. A cet effet, nous posons deux hypothèses:
La première, Hypothèse nulle H0 (hypothèse de non différence). La durée moyenne de séjour en réanimation après une chirurgie abdominale µ1 est égale à la durée moyenne de séjour après une chirurgie vasculaire µ2. Ou les deux moyennes de séjour sont égales µ1 = µ2.
La deuxième est l’Hypothèse alternative H1 (il y a une différence). La durée moyenne de séjour en réanimation après une chirurgie abdominale µ1 est supérieure (ou inférieure) à celle pour une chirurgie vasculaire µ2. Ou µ1≠ µ2 et donc soit µ1 > µ2 ou µ1 > µ2.
Les résultats du test statistique permettent soit d’accepter l’hypothèse nulle, soit de la rejeter.
Un test statistique vérifie l'hypothèse H0
Le principe d’un test statistique consiste à poser une hypothèse sur les paramètres calculés sur l’échantillon (moyenne, pourcentage, variance….) et à examiner si cette hypothèse est vérifiée sur l’ensemble de la population.
Lors d’un test statistique, on définit deux hypothèses sur les populations:
Hypothèse nulle H0 est la première hypothèse posée qui stipule que les séries de données ou les distributions d’où sont tirées les populations sont identiques ou ne sont pas liées. C’est toujours une hypothèse de non-effet (« il n’y a pas de différence entre… », « il n’y a pas de relation entre… »).
En même temps nous posons une autre hupothèse ou:
Hypothèse alternative H1 qui est l’hypothèse à retenir si les résultats du test statistique rejettent l’hypothèse H0.
Car en réalite un test statistique vérifie en premier l’hypothèse nulle H0. Les résultats du test permettent soit d’accépter H0 et donc par exemple les séries de données sont égales µ1 = µ2. Ou alors de rejeter H0 et nous devons accepter l’hypothèse alternative H1. Dans ce cas nous pouvons affirmer que la différence ou la relation étudiée est significative entre les deux populations. Autrement dit, les résultats du test confirment que la différence est trop grande entre les séries pour l’attribuer à un simple hasard ou à une fluctuation d’échantillonnage. Les paramètres des deux population étudiées sont bien différents.
Tests d'hypothèse uni et bilatérale
Hypothèse alternative H1 en bilatérale
L’Hypothèse alternative H1 peut être en uni ou bilatérale selon les objectifs de l’étude établis.
Lorsqu’on ne cherchons pas à connaitre le sens de la différence. On veut juste savoir si les deux séries sont différentes ou pas.
Dans l’exemple ci-dessus, il y a une différence entre la durée moyenne de séjour en réanimation après une chirurgie abdominale et une chirurgie abdominale. µ1 ≠ µ2.
Hypothèse alternative H1 en unilatérale
On soupçonne le sens de cette inégalité, une série est plus grande que l’autre. On cherche une confirmation.
La durée moyenne de séjour en réanimation après une chirurgie abdominale µ1 est supérieur à celle pour une chirurgie abdominale µ2 . µ1 > µ2.
Si cet article vous a été utile, Merci de le partager