P VALUE ET SIGNIFICATIVITE D'UN TEST STATISTIQUE
Tout le monde connait l’importance de la p value ou petit p dans une étude analytique. Cette valeur accompagne toujours les tableaux des résultats statistiques, que ça soit dans les résultats des articles scientifiques ou dans les rapports des études cliniques. Sa grandeur permet de donner de manière synthétique des conclusions sans équivoque. Donc pour bien comprendre les résultats d’une analyse statistique, il faut aussi comprendre la signification de la p-value.
Sommaire
Que signifie la p-value ?
Tout d’abord, la p-value est une valeur qui nous indique si les résultats d’une analyse sont significatifs ou non. Elle est donc calculée lors d’un test statistique.
De toute évidence, elle accompagne les résultats d’un tableau descriptif. Car sa valeur permet de montrer si la différence ou la relation observée entre les paramètres descriptifs est réelle pour l’ensemble de la population. Sans oublier que les paramètres descriptifs sont calculés à partir des données de l’échantillon.
Ainsi pour conclure sur la significativité des résultats d’une analyse, la valeur p doit être comparée à une autre valeur appelée risque d’erreur alpha.
Afin de mieux comprendre la signification de chacun de ces termes, nous allons tout d’abord aborder ci-dessous, certaines notions importantes en statistique. Tel que l’inférence statistique et les risques d’erreur.
Inférence Statistique et p value
Pour commencer, l’objectif d’une étude en recherche clinique est de poser une hypothèse scientifique, puis de la vérifier en analysant les données recueillies. Evidement, cette hypothèse est formulée sur une population donnée (objectif de toute étude), mais l’analyse statistique sera réalisée sur un échantillon de taille réduite.
Par exemple, lors d’une étude menée pour évaluer l’effet d’un nouveau traitement, son objectif vise à traiter toute une population. C’est à dire plusieurs milliers de patients. Seulement il est rare, voir impossible de pouvoir recueillir les données de plusieurs milliers de patients pour les étudier.
Nous devons donc réaliser cette étude sur un échantillon représentatif de cette dernière, mais avec un nombre de patients bien plus réduit. A travers l’analyse statistique de cet échantillon, nous pouvons obtenir des résultats et conclure sur l’ensemble de la population.
L’ensemble des méthodes statistiques appliquées à cet effet s’appellent l’Inférence statistique. Ainsi la p value calculée par le test statistique nous indique si les résultats obtenus dans l’échantillon, sont réels et significatifs pour l’ensemble de la population ou non.
Un petit exemple pour comprendre
Prenons un autre exemple d’une étude d’évaluation d’un traitement pour la réduction de l’Indice de Masse Corporelle IMC (cm/kg²). L’étude est menée dans un échantillon de deux groupes de patients. Le premier groupe reçoit le nouveau traitement et le deuxième un traitement de référence.
La première étape de l’analyse des données recueillies consiste à calculer les paramètres descriptifs. Pour ce critère l’IMC (variable quantitative) nous calculons les moyennes dans chaque groupe de traitement. Je précise bien que les moyennes sont calculées dans les deux groupes de l’échantillon.
Lors de cette analyse descriptive nous observons une différence de moyennes entre les deux groupes. Par exemple la moyenne du groupe1 est inférieure à la moyenne du groupe 2. Mais nous ne pouvons pas affirmer que cette différence est réelle et significative dans la population pour laquelle sont destinés les traitements.
Un Test statistique permet de tester cette différence dans la population.
Donc pour confirmer (ou infirmer) cette différence, nous devons utiliser un test statistique formel, en l’occurrence le test T de Student.
Les résultats de ce test dont la p-value, sont comparés à une valeur seuil fixe que l’on appelle le risque d’erreur α (développer plus loin). Suivant si la valeur p est inférieure ou supérieure à ce seuil, la différence observée est significative ou non dans la population entière de l’étude.
Nous allons supposer pour cette exemple, que la p value calculée est inférieure au risque α. Le nouveau traitement est donc meilleur que le réfèrent pour la population concernée.
Par définition, le risque alpha est le risque de conclure à une différence ou une corrélation entre deux populations alors que cette différence n’existe pas. La différence observée entre échantillons est due au hasard, aux fluctuations des échantillons, aux biais.
Cela dit, pour pouvoir conclure avec certitude à l’existence d’une différence entre deux populations, le résultat du test en l’occurence la p-value doit être inférieur à la valeur seuil du risque alpha . Donc à la valeur de 0.05 si nous avons fixé le risque Alpha à 5%.
Risque d’erreur alpha
Seulement, faire des conclusions sur l’ensemble de la population en se basant sur les données de l’échantillon comporte un certain nombre de risques. Plusieurs facteurs peuvent être à l’origine de ces risques d’erreur de conclure à tord. Les plus importants, sont les biais introduits lors de la recherche et il en existe plusieurs types. Un article est dédié à la notion de biais en recherche clinique. Pour le moment, nous citerons l’exemple du biais de sélection.
Si les sujets inclus dans l’échantillon n’ont pas les mêmes caractéristiques que ceux de la population étudiée. L’échantillon n’est pas représentatif de la population. Nous avons donc inséré un biais de selection. Par concéquent, la caractéristique étudiée est mal mesurée dans la population ce qui induit des erreurs d’évaluation. On conclut à tort à une différence ou une relation qui en réalité n’existe pas.
Donc conclure sur l’ensemble de la population en se basant sur les résultats tirés de l’échantillon, comporte un risque de se tromper. C’est ce que l’on appel le risque de première espèce ou risque d’erreur Alpha α. C’est en définitive le risque de conclure à tord à une différence, alors que cette différence n’existe pas.
Le risque d’erreur α est le risque de conclure à tort à une différence qui n’existe pas.
Ce risque d’erreur légitime doit être accepté et évidemment minimisé. Il est déterminé par le choix de l’expérimentateur mais généralement il est fixé entre 1% et 10%.
Les statisticiens et la communauté scientifique ont fixé ce risque Alpha à 5%, d’où l’Intervalle de Confiance IC95%. Toutefois et quel que soit son seuil, il doit être fixé à priori avant le début de l’étude.
Test Statistique et p value
Nous arrivons à présent au cœur de cet article, expliquer le sens réel de la p-value. Et comme dit précédemment, la p value est le résultat d’un test, d’une analyse. C’est une valeur calculée lors d’un test statistique.
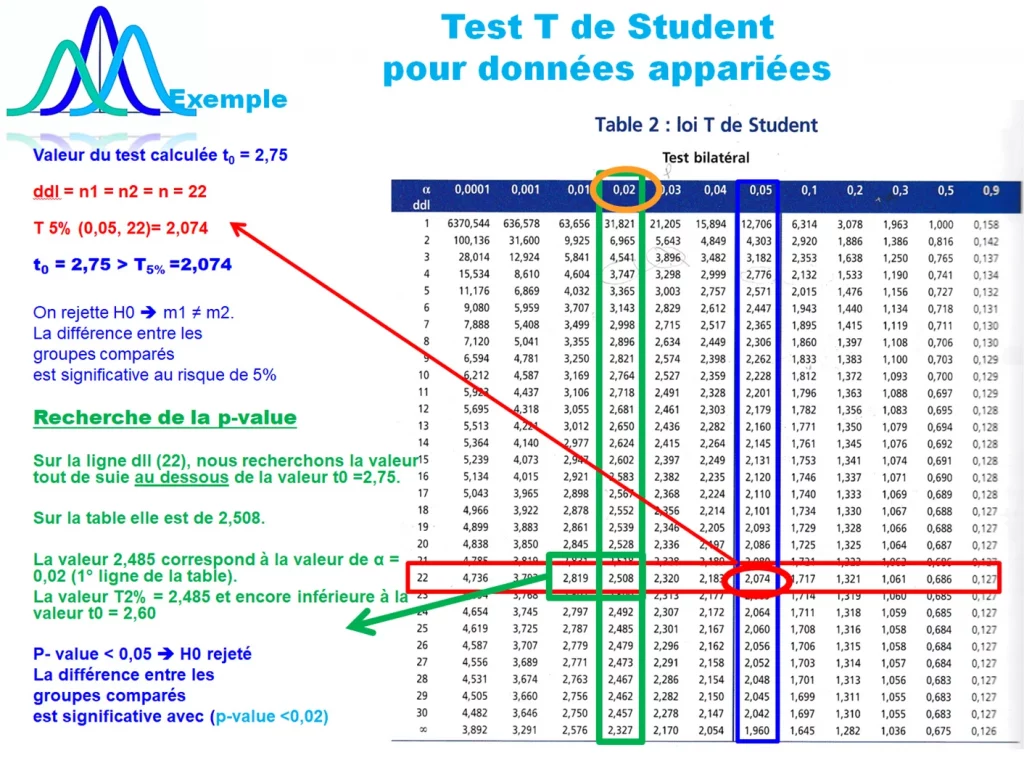
En réalité, le principe d’un test statistique consiste à calculer une expression mathématique sur l’ensemble des données de l’échantillon et de la comparer à une distribution d’une loi théorique connue. Il y a plusieurs en statistique Loi Normale, Loi T de Student, Loi de Fisher ou la loi du χ². En pratique, nous comparons la valeur du test à des valeurs fixes dans une table théorique des nombres, tel que la Table de Student ou Z, table de Fisher ou la table du χ².
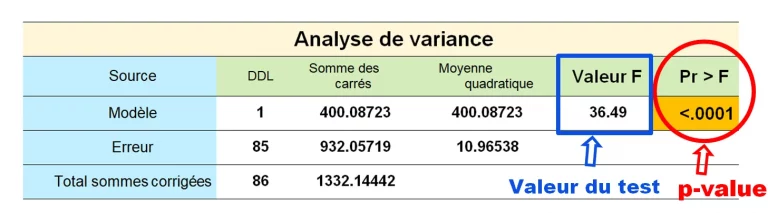
Donc lorsque nous réalisons un test, soit par un logiciel de statistique ou par nos propres calculs, nous obtenons deux résultats. La valeur du test (par exemple la Valeur F dans le tableau ci-dessous) et la p value (Pr > F). Les deux valeurs sont comparées à la valeur seuil du risque alpha, fixée à priori à 5%.
Présentation des résultats d’une analyse statistique
Toutefois et dans le souci de simplifier la lecture des résultats d’un test à l’ensemble des lecteurs, la valeur p est plus représentée et elle est plus considérée. Elle est présente dans les tableaux de résultats et est directement comparée à la valeur alpha α fixe.
Ainsi pour tous les tests statistiques et quelque soit la grandeur de la valeur p calculée, deux résultats sont possibles:
Soit la p-value est inférieure ou égale au risque α, dans ce cas la différence entre échantillons est significative dans les populations.
Soit la valeur p est supérieure au risque α, et de ce fait il n’y a pas de différence (ou de relation) entre les populations de l’étude. La différence observée entre les échantillons est due au hasard.
p-value ≤ α , il y a une différence / corrélation entre les populations.
p-value ≥ α , il n’y a pas de différence / relation entre les populations de l’étude.
Par exemples:
p-value = 0,04 et donc ≤ 0,05, en conclusion, il y a une différence ou une corrélation entre les populations.
– p-value = 0,1 et ≥ 0,05 , nous retenons H0, il n’y a pas de différence ou de relation entre les populations de l’étude.
p value et degrés de significativité de l’analyse
Ainsi en comparant la valeur p calculée à la valeur seuil alpha, nous avons d’ores et déjà le résultat de notre analyse statistique. C’est-à-dire que soit la différence est significative, soit elle est non significative. Nous pouvons nous arrêter là car c’est un résultat suffisant pour conclure.
Mais en réalité, la p valeur donne plus d’information que sa simple comparaison au risque alpha. Sa valeur nous indique plus précisément le degré de risque réel encouru lors de l’analyse des données de l’échantillon. Ce risque peut être diminué au-delà des 5%. Si par exemple la p value calculée est égale à 0.03. Cela veut dire que le résultat du test statistique est significatif, puisque p est inférieur à 5%. Mais plus encore, ce risque est encore diminué à 3%. Par conséquent, nous n’avons plus que 3% de chance de se tromper sur les résultats de cette analyse statistique.
Dans certaines études, la p-value calculée est inférieure à 1% (<0,001). Dans ce cas, il n’y a pratiquement pas de chance de se tromper sur les résultats de cette étude. La différence étudiée est significative au niveau de la population et ce résultat est sures à 99,9%.
p value est le degré de significativité d’un test. Plus sa valeur est petite et moins on a de chance de se tromper sur le résultat du test.
Conclusion
J’espère que cet article vous a aidé à comprendre la significativité de la p-value. Il reste à savoir que cette petite valeur fait beaucoup de débat auprès des scientifiques ces derniers temps. A juste titre, faut-il l’utiliser comme seul arbitre pour accepter ou rejeter une hypothèse ? Est-ce qu’un seuil de significativité fixé à 5% est toujours judicieux ? Quoi qu’il en soit, je vous laisse vous approfondir sur le sujet avec ces articles publiés dans le journal Nature et dans d’autres revues scientifiques.
Si cet article vous a été utile, Merci de le partager