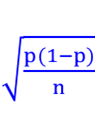Estimation statistique et Intervalle de Confiance
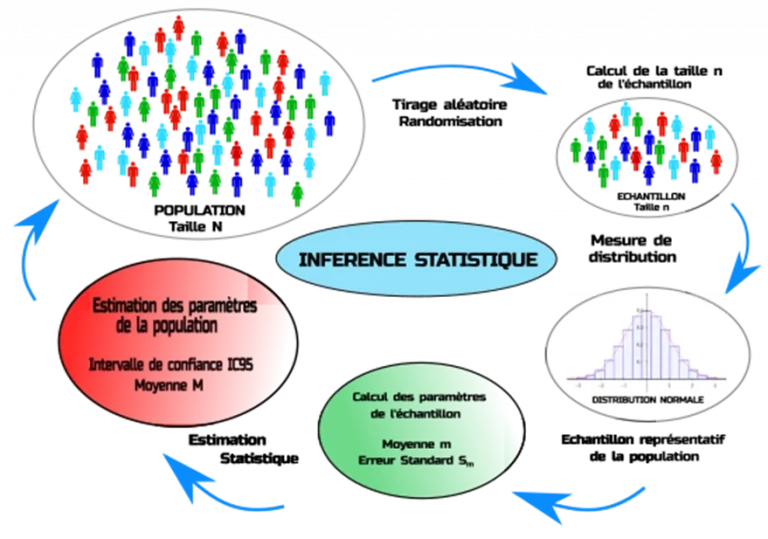
L’ estimation statistique, ou inférence, est l’ensemble des méthodes qui permettent d’estimer les paramètres de la population de l’étude en se basant sur l’analyse des données de l’échantillon.
Sommaire
Estimation des paramètres statistiques
L’objectif d’un projet de recherche est d’étudier une caractéristique, un phénomène ou un facteur dans une population cible. C’est à dire de quelques milliers à quelques millions de sujets ou de patients.
Seulement, il est rare de pouvoir étudier et donc recueillir des données sur la population entière, à moins que cette dernière soit très limitée en raison de ses caractéristiques.
En pratique, nous réalisons l’étude en collectant des données sur un échantillon ou un groupe limité de sujets ayant les mêmes caractéristiques que la population de l’étude. A cet égard, l’échantillon de sujets doit être représentatif de la population dont il est tiré.
Ainsi, les résultats obtenus de l’analyse des données de l’échantillon, nous permettent de conclure sur la population entière. C’est l’estimation ou Inférence statistique.
Que signifie l'Intervalle de Confiance de la population ?
Il de même possible de connaitre les paramètres descriptifs tel que la moyenne et le pourcentage dans la population entière. Le calcul de ces paramètres sur les données de l’échantillon nous permet d’estimer (avec une grande certitude) leurs valeurs inconnues dans la population.
Il est donc possible d’estimer la moyenne et le pourcentage dans la population entière en trouvant un Intervalle dont les bornes permettent de situer avec une grande certitude, Intervalle de Confiance (IC), les paramètres inconnus de la population.
Estimation statistique de la moyenne dans la population
Calcul de Intervalle de Confiance de la Moyenne de la Population IC95%
L’intervalle de confiance IC d’une moyenne calculée sur l’échantillon, est utilisé pour estimer la moyenne inconnu de la population.
Intervalle de confiance (IC) de la moyenne est un intervalle dans lequel la moyenne inconnue M de la population a une grande probabilité de se trouver. A un IC95%, la valeur de la moyenne M dans la population a 95% de chance de se trouver à l’intérieur des bornes de cet intervalle.
IC95% de la moyenne M de la population
m – 1,96 
et m + 1,96
m – 1,96 < M < m + 1,96
Avec
– m est le moyenne calculée dans l’échantillon.
– s est l’écart type dans l’échantillon.
– n est le nombre de sujets ou la taille de l’échantillon.
Intervalle de Confiance du Pourcentage dans la Population
Le pourcentage des sujets dans la population est une valeur contenue dans un intervalle de confiance IC. ou autrement dit, l’Intervalle de Confiance est utilisé pour estimer le pourcentage inconnu dans la population.
IC95% du pourcentage dans la population
p – 1,96 
et p + 1,96
P = p ± 1,96
Avec
– p est le pourcentage calculé dans l’échantillon.
– s = Ecart type dans l’échantillon.
– n est la taille de l’échantillon.
Exemple. Estimation statistique de la moyenne du temps de concentration des enfants
Nous voulons connaitre la moyenne du temps de concentration des enfants de 6 à 10 ans lors du temps scolaire. L’analyse d’un échantillon de 450 enfants d’un département français, a donné une moyenne du temps de concentration égale à 37 minutes et un écart type de 10,2 minutes.
Nous allons estimer la moyenne du temps de concentration des enfants dans la population française dans un Intervalles de confiance à 95%.
Nombre d’enfants dans l’échantillon : n = 450
Moyenne dans l’échantillon : m = 37 minutes
Ecart type : s = 10,2 minutes
L’intervalle de confiance IC95% = m – 1,96 < M < m + 1,96
IC95% est de 37 ± 1,96 x = 37 ± 0,942.
La moyenne du temps de concentration du temps scolaire des enfants français est entre 36,058 et 37,942.
Conclusion
