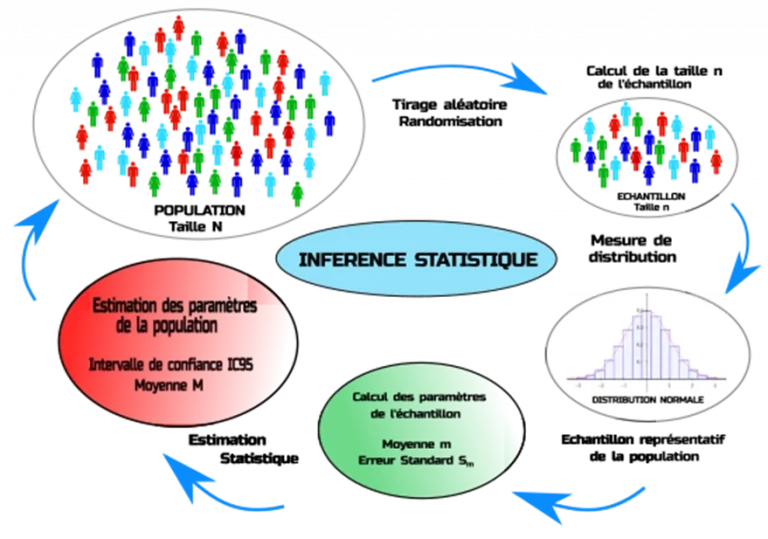
STATISTIQUE INFERENTIELLE
Une analyse statistique est composée de deux étapes, une analyse descriptive suivie de statistique inférentielle. Par l’intermédiaire de l’analyse descriptive réalisée à partir des données de l’échantillon, nous pouvons observer une différence (ou une relation) entre, par exemple les moyennes des deux groupes de sujets. A travers une inférence statistique et la réalisation d’un test, que nous pouvons savoir si cette différence observée est réelle et significative dans la population de l’étude.
Sommaire
Statistique inférentielle est l'extrapolation des résultats de l'échantillon à la population
Par définition, les statistiques inférentielles sont l’ensemble des méthodes statistiques permettant de généraliser ou inférer les résultats tirés de l’échantillon à l’ensemble de la population.
Pour commencer, il est à noter qu’il est souvent difficile, voire impossible d’étudier un facteur ou une caractéristique sur l’ensemble de la population. Car quel que soit cette population, le nombre de sujet qui la constitue est très élevé. Il faut donc mener l’étude sur un échantillon avec un nombre de sujets restreint. Evidement, l’échantillon de l’étude doit être représentatif de la population concernée. C’est à dire que les sujets à sélectionner doivent avoir les mêmes caractéristiques que la population visée.
Ainsi après analyse, les paramètres descriptifs comme la moyenne, le pourcentage et tous les résultats des tests calculés sur les données de l’échantillon pourront être extrapolés à l’ensemble de la population. C’est le cas par exemple de l’estimation statistique comme le calcul de l’Intervalle de Confiance (IC95%) de la population. C’est aussi la détermination de la p-value ou significativité du test statistique que nous avons appliqué. Ces derniers calculs sont donc des méthodes d’inférence statistique.
Notions d'échantillon et population - Définition
Population:
C’est un ensemble d’individus semblables, ayant les mêmes caractéristiques et appartement à un même endroit. Et dans ce cas faisant l’objet d’une étude.
Echantillon:
C’est un groupe d’individus choisit au hasard dans la population. Evidement l’échantillon doit étre représentatif de la population. Ce qui veut dire que les individus doivent avoir les mêmes caractéristiques. L’échantillon doit être l’image réduite et fidèle de la population qu’il représente.
La qualité principale de l’échantillon c’est qu’il doit être REPRESENTATIF DE LA POPULATION. Car lorsque l’échantillon n’est pas représentatif de la population, il fournit DES RÉSULTATS BIAISÉS.
Statistique Inférentielle et estimation des paramètres de la population
Lors d’une étude expérimentale, il est toujours important de décrire les données de l’échantillon avec des paramètres descriptifs comme la moyenne ou le pourcentage selon les groupes à comparer. Mais il est aussi très important de connaitre et représenter ces paramètres descriptifs dans la population de l’étude.
Par exemple, nous voulons déterminer la taille moyenne des enfants de 3 à 6 ans dans la population Française. Connaitre ce paramètre dans la population est très utile et nous permet de déterminer la croissance de n’importe quel enfant dans cette tranche d’âge. Pour cet effet, nous pouvons calculer la moyenne de la taille des enfants à partir d’un échantillon. Puis calculer ensuite la moyenne dans la population grâce à l’Inférence.
L’inférence statistique permet donc de détermination des paramètres d’un facteur ou d’une caractéristique donnée dans la population à partir de l’analyse des données d’un échantillon.
Par contre, déterminer la valeur exacte d’un paramètre dans la population entière est impossible. Il est cependant estimé entre deux valeur dans un Intervalle de Confiance.
Donc l’analyse descriptive des données d’un échantillon permet de calculer la moyenne ou le pourcentage de la population dans un intervalle de confiance.
L’estimation statistique de la moyenne ou d’un pourcentage de la population par l’Intervalle de Confiance est un autre outil des Statistiques Inférentielles permettant d’extrapoler les résultats de l’analyse de l’échantillon à l’ensemble de la population.
Pour en savoir plus sur l’estimation statistique et la détermination des paramètres de la population et vour notre article IC95% . Toutes les explications et les méthodes de calculs avec des exemples simple mais bien concrets.
Inference et test statistique
L’objectif d’un test statistique est de vérifier si la différence ou la relation observée entre les moyennes ou les pourcentages calculés dans l’échantillon est significative. Le terme de significative veut dire que cette différence ou relation est réelle pour l’ensemble de la population étudiée. De la même manière, la p value calculée par le test statistique nous indique si les résultats obtenus dans l’échantillon, sont vrais et significatifs pour l’ensemble de la population ou non.
Dans l’exemple ci-dessus, les moyennes du groupe Traité et Contrôle sont bien différentes dans l’échantillon. La p-value = 0,005 du résultat du test statistique montre bien que cette différence est significative pour l’ensemble de la population.
Si cet article vous a été utile, Merci de le partager