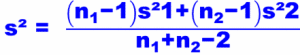Test de Student sur Excel ou test T fonction de calcul de la p-value

Comment réaliser le Test T de Student sur Excel ?

Le test T de Student est un test statistique, très utilisé pour comparer les données quantitatives. Il est utilisé pour comparer les moyennes de deux groupes de sujets. Cependant il existe deux types, un pour données appariées et un autre pour données indépendantes. Les deux tests sont facilement réalisables sur Excel. Dans cet article, nous expliquerons le principe géneral du test de Student, ensuite nous détaillerons chaque test séparément. Nous verrons aussi les détails de leurs calculs et l’interpretation de leurs résultats. Mais aussi la fonction de calcul du Test de Student sur Excel qui permet de donner directement la p-value. Et enfin les conditions d’application très importantes qui conditionnent leur utilisation.

Sommaire

Principe du Test T de Student

Le test T de Student en général est applicable pour comparer des variables quantitatives. Nous utiliserons ce test pour:

Comparer la moyenne d’un échantillon à une moyenne théorique.
Comparer deux séries de données ou deux groupes de sujets en comparant leurs moyennes m1 versus m2.
Il test aussi le coefficient de corrélation lors d’une analyse de corrélation.

Il existe en effet deux « types » de tests de Student, un pour donnés appariées et un autre pour données indépendantes.
La différence entre les deux réside uniquement dans la formule de calcul de la valeur du test. Plus particulièrement au niveau du dénominateur de la valeur du test et dans le dll ou degrés de liberté qui accompagne la formule du test. Nous détaillerons plus bas les étapes de calcul et la fonction de réalisation de chaque test séparément.

Mais tout d’abord nous devons exposer les conditions d’application du test de Student en général. Car ce dernier est un test paramétrique. Pour pouvoir l’appliquer, il faut que les données ou les groupes à analyser suivent une distribution normale. Cette condition de normalité est toujours applicable lorsque nous analysons des données quantitatives. Que ça soit pour comparer des moyennes, des variances (cas de l’ANOVA) ou pour rechercher une relation lors d’une analyse de corrélation.

Une autre condition existe lorsque les deux séries à comparer sont indépendantes. Cette condition est l’égalité des variances ou homoscédasticité des deux séries de données.

Séries indépendantes (ou paralléles) et séries appariées

Tout d’abord pour toutes les explications ci-dessous, je désigne par deux échantillons de données à comparer différents termes, tel que deux séries, deux groupes de traitement ou deux variables. Tous ces termes désignent la même chose.

Séries indépendantes ou groupes parallèles

Données ou deux séries Indépendantes sont deux échantillons de données à comparer et mesurés chez des sujets différents. Cela signifie que la série1 est constituée de manière indépendante de la série2 (par opposition aux échantillons appariés). Cela veut dire encore que les sujets de la série1 ne sont pas les mêmes que ceux de la série2. Les deux séries peuvent avoir des effectifs différents. Chaque série à un nombre de sujets différents. Le nombre de sujets de la série1 = n1 et celui de la série2 = n2. Ces deux nombres peuvent être différents.

Par exemple nous voulons analyser le taux de glycémie chez deux groupes de sujets, malades et sains. La série1 constitue le groupe de malades alors que la série2 constitue les données du groupe des sujets sains. Le taux de glycémies à comparer sont mesurés chez le groupe de malade d’une part et dans le groupe des sujets sains d’autre part. Nous utiliserons le test T en indépendant car les données des deux groupes sont indépendants.

Séries appariées ou données intra individuelles

Les données appariées sont mesurées chez un même sujet. Par exemple pour comparer les données mesurées avant et après un traitement ou, comparer les mesures réalisées sur le côté droit versus le côté gauche chez le même sujet. Dans le cas des données appariées, le nombre d’observation de la série1, n1 est égale au nombre d’observation de la series2, n2 qui est égale au nombre Total des sujets de l’échantillon n. C’est à dire que n1 = n2 = n.

Test T pour données indépendantes

Comme nous l’avons déjà expliqué dans d’autres articles de notre blog, le principe d’un test statistique consiste à calculer une expression mathématique sur les données de l’échantillon et de la comparer à une distribution d’une loi théorique connue.

Nous calculons aussi les paramètres descriptifs des données de l’échantillon. En l’occurrence les moyennes m1 et m2 et l’écart types et/ou les variances de chaque série à comparer. Ces derniers nous serviront à calculer la valeur du test T.

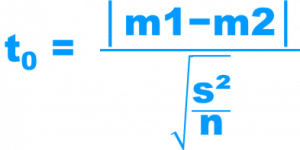
Valeur du test de Student pour données indépendantes et son dll

avec: degrés de liberté dll = n1 + n2 -2

s² est la variance des deux séries de l’échantillon qui est calculable avec la formule :

m1 et m2 = moyennes des deux séries à comparer

n1 et n2 = Tailles des deux séries dans l’échantillon

s²1 et s²2 variances de chaque groupe.

Tous ces paramètres sont facilement calculables avec les formules de MS Excel. Il suffit juste de bien sélectionner les données de chaque série séparément.

Pour les moyennes =moyenne(A1;A30)

Effectif d’une série =NB(A1;A30)

Ecart type =ecarttype(A1;A30)

Variance =variance(A1;A30), Attention la variance s² de la formule du test est une variance commune. Il faut la calculer en utilisant la formule ci-dessus.

Interprétation du résultat du test T en indépendant

Significativité du test

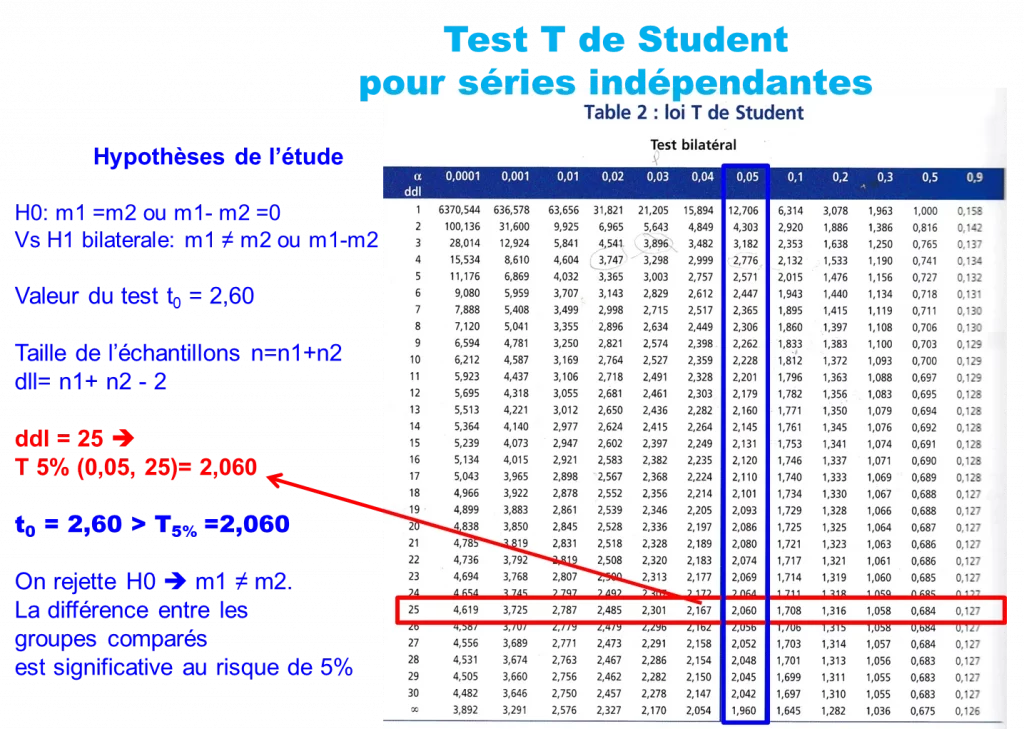
Une fois que la valeur du test t0 est calculée, nous comparons cette dernière à la valeur théorique au risque de 5% ou T5% de la table de distribution de la loi T de Student. Deux résultas sont possibles:

Soit t0 < à T5% (de la table de Student), nous accepterons H0. Il n’y a pas de différence entre les moyennes m1 et m2 des deux populations.
Soit t0 ≥ à T5% (de la table T) nous rejetons donc H0, H1 est vraie. Dans ce cas, la différence entre les deux moyennes m1 et m2 est statistiquement significative.

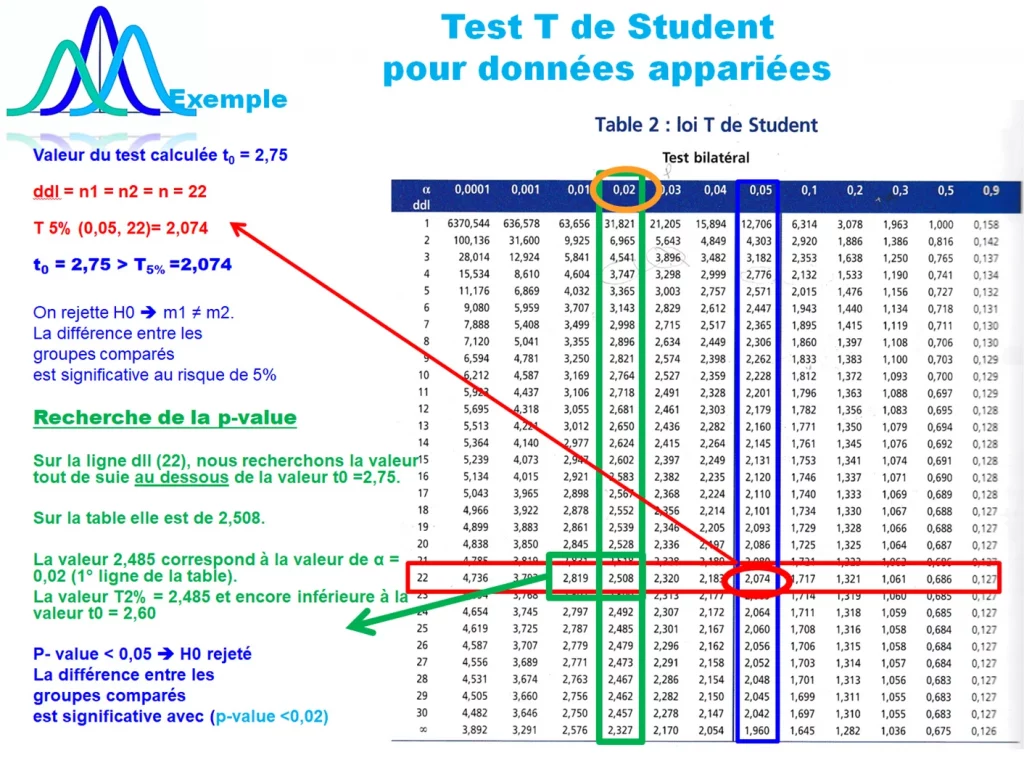
Exemple de résultat du test sur la table de Student

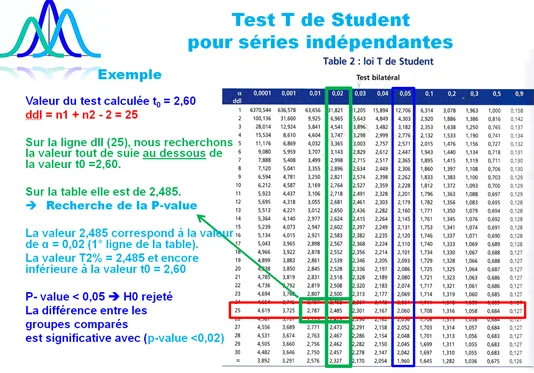
Il est tout à fait possible de chercher directement la p-value dans la table de Student. Pour savoir comment, suivre les étapes dans les tables ci-dessous. Et pour mieux comprendre le sens de la p-value, regardez l’article dédiée à cet effet.

Recherche de la p-value du test en indépendant

De la même manière, nous aurons deux résultats:

Soit la p-value > 0,05 et nous acceptons H0.
Ou alors la p-value ≤ 0,05, nous rejetons H0, H1 est vraie. La différence entre les deux moyennes m1 et m2 est statistiquement significative à p-value = .

Cependant, il est possible de faire encore plus simple et calculer la valeur p ou p-value du Test de Student sur Excel avec la fonction T.Tests pour le test en indépendant. Voir les fonctions Excel ci-dessous.

Test de Student pour données appariées

Exactement comme pour le cas du test pour données indépendantes, nous devons calculer la valeur de ce test pour données appariées puis comparer sa valeur à la valeur Tà 5% dans la même table de Student.

Valeur du test de Student pour séries appariées

avec dll = n – 1

m1 et m2 = moyennes des deux séries à comparer

n = n1 = n2 = Le nombre de sujet dont les séries de données à comparer

S² = variance de la différence entre les deux séries et Erreur standard Sd =

On compare la valeur t0 calculée à la valeur théorique T5% de la table de distribution de la loi T de Student.

L’interprétation du test est identique à celle du test T de Student pour données indépendantes. C’est exactement la même étape d’interprétation de la significativité du test. (voir Interprétation du résultat du test T en indépendant)

Significativité du test T de Student

Les étapes de recherche de la significativé et de la p-value du test T en apparié est exactement la même que celle du test T en Indépendant. La seule différence réside dans la valeur du dll = degrés de libérté. Voir l’exemple dans la table ci-dessus.

Test de Student avec la Fonction T.Test Excel

Vous pouvez réaliser le Test T de Student sur Excel avec la fonction T.Test qui donne directement la p-value. Cette fonction est identique que ça soit pour données indépendants ou pour données appariées.

=T.TEST(matrice1;matrice2 ; uni/bilatéral ; type)

matrice1,matrice2 = série1 et série2 à comparer

uni/bilatéral =test d’hypothèse en unilatérale =1; en bilatérale =2 . Nous considérons pour ce cas que le test est en hypothèse bilatérale.

Type ou type de données : 1=échantillons en appariée : 2 = deux échantillons indépendants et de variance égale et 3 = deux échantillons indépendants et de variances différentes (hétéroscédasticité).

Fonction Excel du Test de Student en indépendant

=T.TEST(série1;série2;2=Bilatéral;2=indépendant)

=T.TEST(série1;série2;2;2)

Fonction Excel du Test de Student en appariées

=T.TEST(série1;série2;2=Bilatéral;1=Apparié)

=T.TEST(série1;série2;2;1)

ATTENTION La fonction T.TEST donne directement la p-value

Conditions d’application

La condition la plus importante pour le test de Student, aussi bien en apparié qu’en indépendant est la normalité des deux séries de l’échantillon. Si par contre les séries de données à comparer ne suivent pas une loi normale, il faut utiliser un test équivalent non paramétrique tel que le test de Wilcoxon ou test de Mann Whitney.

Par contre la condition de l’égalité des variances n’est applicable que dans le cas du test T de Student pour données indépendantes. En effet dans le cas des données en appariées les deux séries proviennent du même échantillon de sujets. Les mesures sont réalisées chez les mêmes individus, ce qui réduit la variabilité due aux individus.