Analyse de corrélation
Les différentes tests d'analyse de corrélation
Comme pour les tests de comparaison, le type de test dépend de la nature des variables à analyser. Plusieurs tests de corrélation existent.
Sommaire
Corrélation entre variables qualitatives
Si vous cherchez à étudier la relation entre deux ou plusieurs variables qualitatives, il faut utiliser le test de Khi-2 d’indépendance. Ce test a le même principe et les mêmes calculs que le test du Khi-2 de comparaison de pourcentages. Il est à appliquer pour chercher par exemple une éventuelle relation entre le taux de guérison et le type de traitement administré ?
Analyse de corrélation entre deux variables quantitatives
Par contre pour l’étude d’une liaison entre deux variables quantitatives, le test de corrélation à appliquer est une analyse de régression linéaire. Ce test fait l’objet de cet article et il est relativement simple. Nous expliquerons ici son principe, ses calculs et sa réalisation sur Excel.
Recherche de relation entre variables quantitative et qualitative
Cependant, pour une analyse de corrélation entre une variable quantitative et une autre qualitative, vous devez utiliser une analyse de variance ANOVA. Ce test est applicable de la même manièrele que pour comparer entre plus de trois variables quantitatives.
Analyse de corrélation en multivarié
Pour l’ensemble des trois tests ci-dessus, l’analyse est en univariée. Mais il est souvent utile d’étudier une relation entre variables en incluant d’autres facteurs dans l’analyse. Nous devons utiliser à cet effet une analyse en multivariée. A cet effet nous devons appliquer des tests plus avancés comme par exemple la régression logistique ou l’analyse de régression en multivariée.
Principes de l'analyse de corrélation entre variables quantitatives
Exemple Etude de la relation entre le poids (kg) et la taille (cm)
Comme d’habitude, nous commençons l’explication du test par un petit exemple très classique. Il nous permettra de comprendre ce que nous cherchons exactement à faire.
Nous voulons savoir si le comportement d’une variable, le Poids en Kg est influencé par les valeurs d’une autre variable, la Taille en cm. Le poids et la taille sont deux variables quantitatives et elles sont mesurées chez le même individu.
En premier lieu et pour étudier cette relation, nous pouvons déjà porter les données des deux variables sur un graphique. Nous traçons donc la relation entre le poids et la taille en représentant: La variable X, la taille en abscisse et la variable Y donc le poids en ordonnée.
Soit pour un individu donné mesurant 172 cm, il pèse 66 kg.
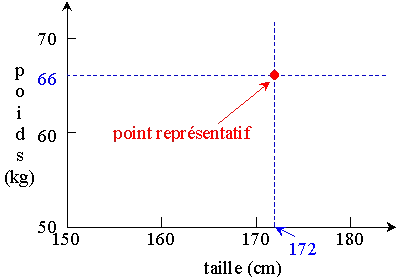
En représentant tous les individus de l’échantillon nous obtenons un graphique en nuage de point.
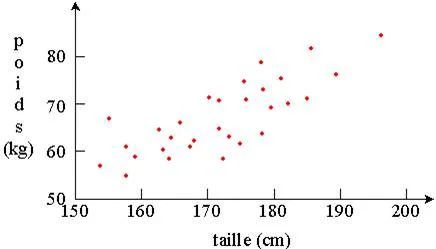
L’aspect du nuage est allongé. Nous pouvons même envisager de tracer une droite qui passe au milieu du « nuage » et au mieux par le maximum de points.
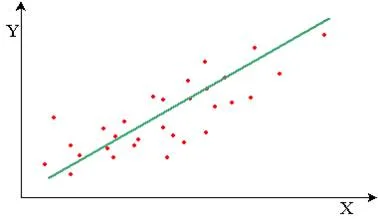
En traçant la droite nous constatant que les points ont une tendance linéaire. Le poids et la taille ont donc une liaison linéaire.
Leur liaison est « ascendante » car la droite « monte ». Ce qui veut dire que quand la taille augmente, le poids augmente.
C’est une corrélation linéaire ascendante ou positive
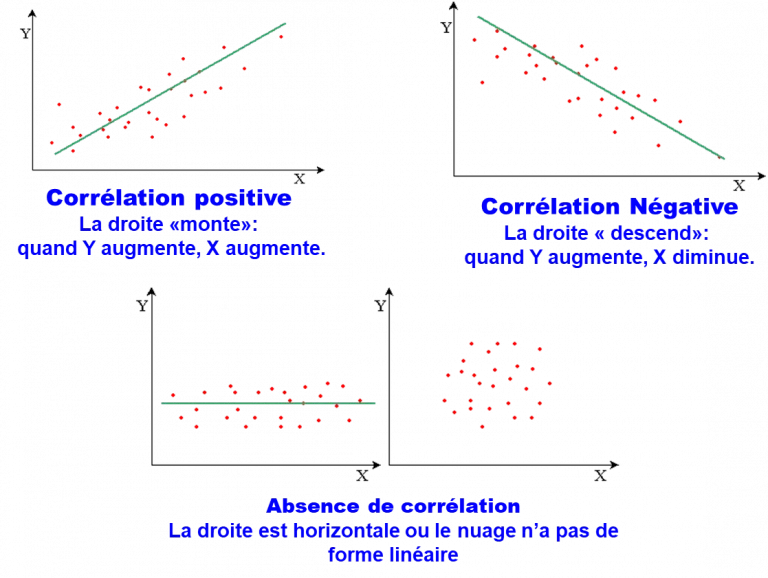
Exemples de types de corrélation linéaire
Analyse de corrélation et Régression Linéaire
L’analyse de corrélation entre deux variables quantitatives est une analyse de régressions linéaire En effet une fois que nous avons tracé le nuage de points, nous devons tracer la droite qui passe par le maximum de points. Seulement pour un même graphique, et si par exemple nous devons tracer la ligne à la main, nous aurons une infinité de droites. Ceci veut dire que pour chaque droite tracée, les paramètres de celle là seront différents.
Droite de régession
Cependant, il existe une méthode mathématique pour déterminer la « meilleure » droite qui passe au mieux par tous les points en minimisant les écarts des points représentatifs de cette droite. Cela veut dire que la droite est tracé de telle manière que la somme des carrés des écarts d1, d2,… di soit minimale.
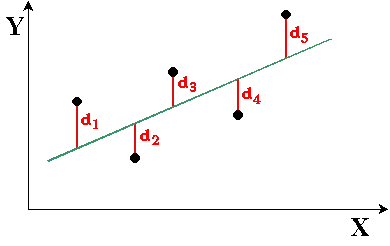
Cette méthode s’appelle la Méthode des moindres carrés ∑di² = minimum
La droite des moindre carrés est appelée: DROITE DE REGRESSION
Fonction de la droite de Régression Linéaire
En traçant la droite du nuage de point, nous avons modélisé la relation entre les deux variables X et Y par une fonction linéaire, celle d’une droite de régression de type:
Y = a X + b
a est la pente de la droite et b est l’ordonnée à l’origine
Une fois les paramètres a et b de la droite sont estimés à partir des données de l’échantillon, nous pouvons prédire les valeurs d’une variable en connaissant les valeurs de l’autre variable.
Par exemple, nous pouvons estimer une valeur de Y connaissant une valeur de X et inversement.
Nous pouvons aussi estimer la valeur moyenne de Y pour une valeur moyenne de X.
Et enfin, nous pouvons estimer la valeur y d’un individu présentant une valeur X.
En plus, la pente de la droite a, donne le sens de la corrélation. Par contre il ne donne pas sa qualité. Par exemple si:
- a > 0 corrélation positive: X et Y varient dans le même sens.
- a < 0 corrélation négative: X et Y varient dans des sens opposées.
- a = 0 pas de corrélation.
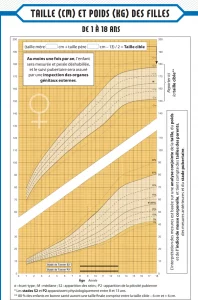
Un exemple très concret de cette relation, est celui de la courbe de croissance Poids et Taille du carnet de santé des enfants. En comparant la taille d’un enfant dans la courbe, nous pouvons avoir son poids idéal et donc une estimation de sa croissance. Ces courbes ont été tracées par les chercheurs des organismes compétants INSERM en analysant des grosses bases de données type Big Data .
Coefficients de la droite de régression
Pour calculer les paramètres a et b de la droite de régression, il y a des formules mathèmatiques à appliquer. Je les donne ici juste à titre d’information, même si il est tout à fait possible de les calculer grace aux données. Evidement, nous pouvons faire plus simple et les calculer par une fonction de MS Excel. Nous verrons cela plus bas.
Pente de la droite de régression a:
La pente de la droite : 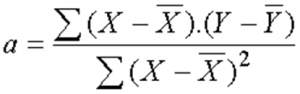
Ou pour une formule plus détaillée: ![]()
Comme je l’ai déjà mentioné, ces formules mathématiques ne sont pas aussi complexes que ce que l’on pourrait croire. Car il suffit de remplacer X1, X2, …,Xn et Y1, Y2, …., Yn par les valeurs ou les données des variables X et Y dans l’échantillon.
¯X et ¯Y ou X et Y barre sont les moyennes des variables X et Y de la base de données de l’échantillon. Nous pouvons aisément les calculer sur Excel. D’ailleurs les deux paramètres seront calculés automatiquement par une fonction de MS Excel.
Ordonné à l’Origne b de la droite :
L’ordonné à l’Origne: 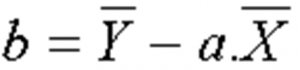
De la même manière le paramètre b peut être calculé directement par la fonction MS Excel.
Coefficient r de l'Analyse de Corrélation
Comme je l’ai écris plus haut, le paramètre a de la droite donne le sens de la corrélation, mais pas sa qualité. Nous devons à présent déterminer la qualité de cette corrélation. En d’autres termes, nous devons mesurer la force de la liaison ou le degrès de relation entre les deux variables. Le calcul du coefficient de corrélation nous permet d’arriver à cet effet.
Coefficient de corrélation r = 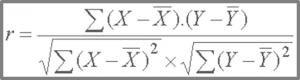
X et Y sont les valeurs des variable X et Y respectivement.
¯X et ¯Y moyennes de X et Y.
En toute évidence, d’autres formules existent. Elles sont plus ou moins complexes, mais donnent exactement le même résultat.
Pour vous rassuer et comme pour les autres paramètres de la droite, le coefficient de corrélation peut être calculé automatiquement sur Excel ou sur n’importe quel logiciel Statistique.
Coefficients de Pearson et Spearman
Le coefficient de corrélation s’appelle coefficient de Pearson. Il est applicable quand les données des deux variables suivent une distribution Normale (voir ci-dessous).
Quand les données ne sont pas normaux (distribution non Gaussienne), nous pouvons mesurer la force de la relation entre les deux variables avec le coefficient de Spearman qui est un coefficient Non paramétrique. Pour plus d’information sur le coefficient « Rho » de Spearman, lisez cet article..
Carractèristiques du coefficient de corrélation
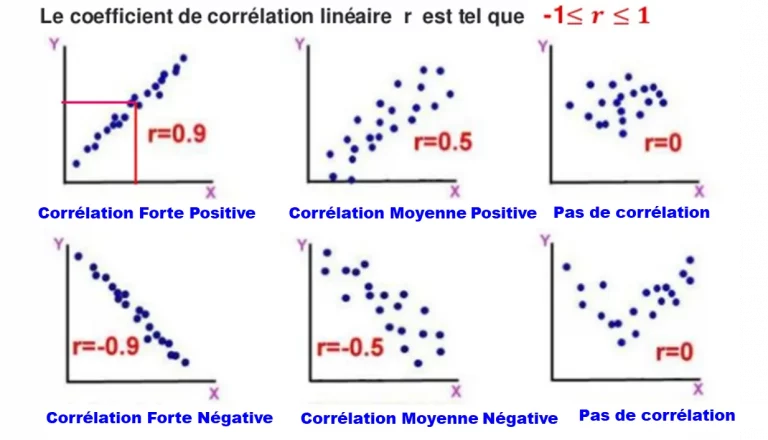
Le coefficient r calculé est toujours compris entre -1 et 1. Il est sans unité de mesure. Il faut savoir que plus r est proche de la valeur absolue |1|, plus la liaison entre les deux variables est forte. Voici quelques exemples:
- Si r = +1 la corrélation entre les deux variables est positive parfaite (très forte).
- Si r = -1 la corrélation est négative parfaite.
- Si r = 0, absence totale de corrélation linéaire.
r est exprimé en puissance 2 c’est à dire en R²
Quelques exemples de la qualité de la corrélation
Test de l'Analyse de corrélation
Pour résumer tous ce que nous avons faits jusqu’à présent.
En cherchant une éventuelle relation entre deux variables quantitatives X et Y de notre échantillon, nous avons,
Premièrement, modélisé cette relation entre les variables par une fonction linéaire Y = a X + b.
Deuxièmement, calculé les paramètres a et b de cette droite de régression. Ces deux paramètres sont importants pour prédire les valeurs d’une variable en fonction de l’autre.
Ensuite, nous avons mesuré le degré de cette relation en calculant le coefficient de corrélation r.
Bien entendu, tous ces paramètres ont été calculés à partir DES DONNES DE L’ECHANTILLON. Nous ne savons pas encore si cette relation est réelle et significative pour l’ensemble de la population.
Nous devons vérifier la significativité de cette corrélation par un test statistique.
Test de corrélation
En posant comme à chaque fois les Hypothèses de l’étude:
- Hypothèse nulle H0 : r= 0 ; il n’y a pas de liaison entre X et Y.
- Hypothèse alternative en bilatérale H1 : r ≠ 0 ; il y a une liaison (positive r > 0 ou négative r < 0) entre les deux variables.
La valeur du test de Corrélation est :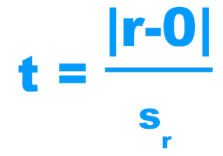
ou

Comme tout test statistique, la valeur du test est toujours accompagnée d’un degrè de liberté dll.
Pour le test de corrélation le dll = n-2.
Sr est l’écart type du coefficient r qui est facilement calculable avec ![]()
n est la Taille de l’échantillon et r = coefficient de corrélation.
Significativité du test de corrélation
Une fois que nous avons calculé la valeur du test de corrélation, nous devons à présent comparer cette valeur à la valeur t à 5% dans la table T de Student. Exactement de la même manière que pour le test T de Student.
Si t < T5% (Table de Student) , H0 retenue. Ce qui veut dire qu’il y a absence de liaison significative entre X et Y.
Si par contre t ≥ T5% (Table de Student) dans ce cas, H0 rejetée. Et nous pouvons affirmer qu’il y a une liaison significative entre X et Y. Il faut après chercher la valeur de la p-value dans la table T.
Mais encore nous pouvons faire plus simple et chercher directement la p-value dans la table T de Student.
Ensuite il suffit de comparer la valeur p directement à la valeur du risque alpha (normalement de 0,05).
Si p-value > 0,05 , On accepte H0.
Si p-value ≤ 0,05 on rejette de H0, H1 est vraie.
Recherche de la p-value pour le test de corrélation
Conditions d'application du test de corrélation
Comme pour le test T de student, le test de corrélation obéit à des conditions d’application. Evidemment, les deux variables dont on veut étudier la liaison sont de type quantitatif. Il faut que toutes les deux soient aléatoires et de distribution Normale.
Mais aussi les deux variables doivent être de type appariées. Ce qui veut dire que pour chaque individu i de la base de données, il y a une valeur yi de la variable Y et une valeur xi de la variable X.
Enfin, l’association entre X et Y doit être linéaire et modélisée par une droite de régression linéaire.
Coefficient de Pearson et rho de Spearman
Le coefficient de Pearson est calculé lorsque les données suivent une distribution normales. Alors que le Coefficient de Spearman ou Rho de Spearman est normalement calculé dans le cas contraire, losque les données ne sont pas Gaussiennes.
Intérêt de l'analyse de corrélation
En résumé, une fois que nous avons trouvé que le test de corrélation entre les deux variables est statistiquement significative selon un modèle de régression linéaire de type Y = a X + b, nous pouvons utiliser ce modèle à des fins prédictives dans la population.
En d’autres termes, nous pouvons estimer une valeur de Y connaissant une valeur de X et inversement. Estimer la valeur moyenne de Y pour une valeur moyenne de X et inversement. Et en fin, estimer une valeur yi d’un individu présentant une valeur Xi et inversement.
Analyse de corrélation sur Excel
Comme indiqué plus haut, l’analyse de corrélation entre deux variables quantitatives avec un modèle de régression linéaire est très simple sur Excel. La recherche de cette modélisation se fait quasiment avec la fonction graphique du nuage de point. Pour pouvoir suivre les étapes de cette modélisation, nous reprenons l’exemple cité précédemment, celui de l’analyse du Poids et de la Taille.
A cet effet, nous voulons donc vérifier l’existence d’une relation entre la taille (en cm) et le poids (en kg) des enfants de 2 ans dans un échantillon de 15 sujets.
- Nous posons les variables taille en X abscisse et poids Y en ordonnées. Les 2 variables sont de type quantitatif apparié. Ce qui veut dire que pour une mesure poids, une mesure la taille réalisée pour chaque sujet.
- Nous considérons que le poids et la taille suivent une loi normale.
- Les données sont enregistrées dans une feuille Excel. Nous procédons aux calculs des paramètres descriptifs telle que la moyenne pour des deux variables. Ce calcul n’a pas d’impact sur l’analyse.
Graphique du nuage de point sur Excel
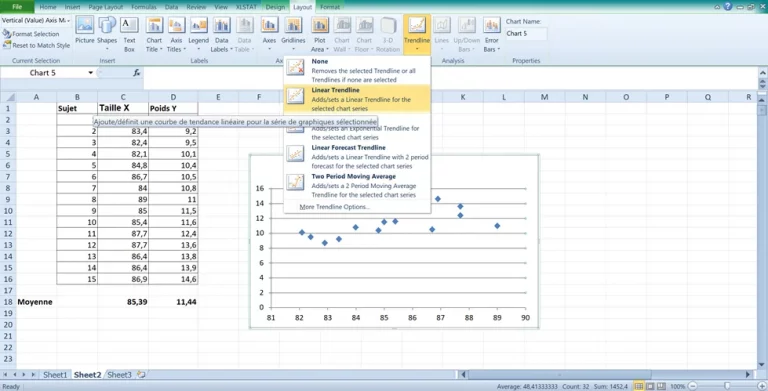
Tout d’abord, nous cherchons à tracer la relation entre le poids et la taille par un tracé en nuage de points. Pour cela dans l’onglet insertion et graphique chercher et cliquer sur « Nuage de point ».
Droite de régression su Excel
Pour tracer la droite de régression, il faut tout d’abord sélectionner le graphique, ensuite « Ligne de Tendance » et dans la liste déroulante sélectionner « Ligne de tendance linéaire ».
A ce moment apparaitra sur le nuage de point le tracé de la droite.
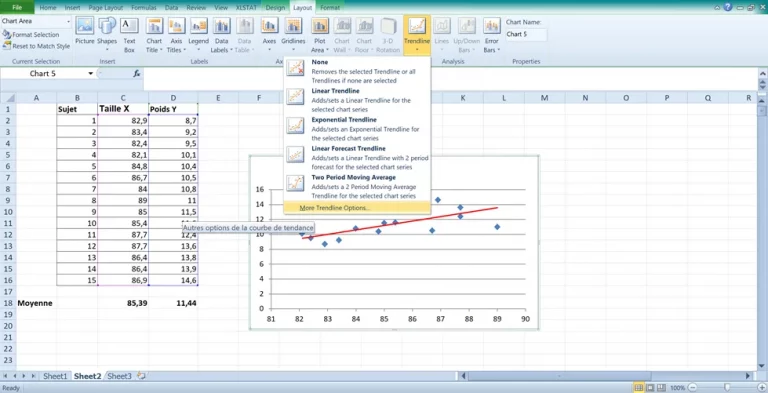
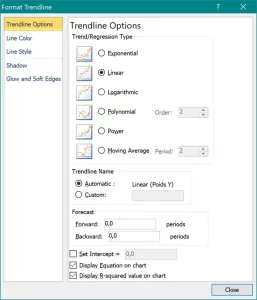
Une fois que la droite de régression est tracé et sur le même onglet » Ligne de Tendance » tout en bas de la liste déroulante, cliquez sur « Plus d’Option ». Dans la fenêtre qui apparaitra, sélectionner « Linéaire », « Afficher l’équation de la droite » et enfin « Afficher le coefficient R² ».
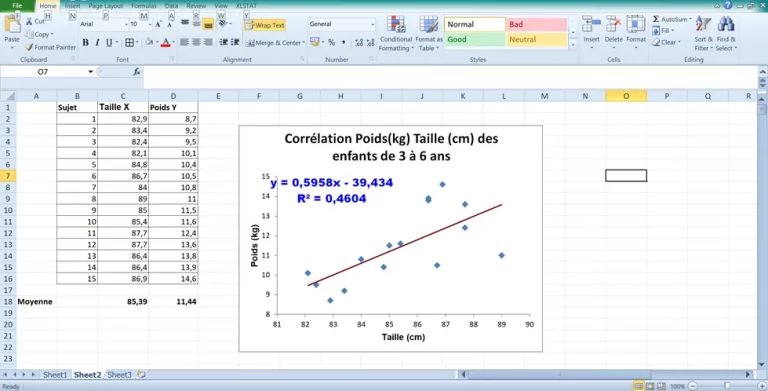
Au même moment cette étape sur Excel calculera le Coefficient de Corrélation exprimé en R². Dans notre échantillon il est égal à 0,4604. La racine carrée du R² donne le coefficient r égal à 0,6785. Il est aussi possible de laculer le coefficient r avec la fonction =Correl(données taille; données poids).
Enfin, vous pouvez améliorer votre graphique en adaptant et en ajoutant des légendes dans les axes des abscisses et des coordonnées ainsi qu’un titre au graphique.
Test du coefficient de corrélation
A partir des données de l’échantillon, l’application Excel a donné la droite de régression, les coefficients de la droite ainsi que le coefficient de corrélation de la relation poids et taille. Il reste à faire le test du coefficient de corrélation pour voir si cette corrélation est significative et qu’elle est extrapolable à l’ensemble de la population. Le test est facilement réalisable en appliquant la formule du test de corrélation décrit ci-dessus.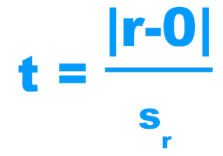
Si cet article vous a été utile, Merci de le partager