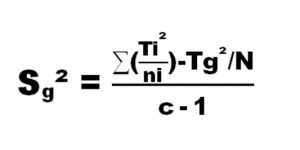ANOVA Analyse de variance
Test global
ANOVA ou ANalyse Of VAriance est un test statistique d’Analyse de variance. Il permet de comparer des séries de données quantitatives en comparant leurs variances. Ce test s’applique pour comparer globalement TROIS séries ou plus en utilisant un test unique de Fisher-Snedecor. C’est aussi un test paramétrique qui s’applique quand les séries de données ont une distribution normale et de variances égales. L’ Analyse de variance ANOVA est utilisé non seulement pour comparer plusieurs groupes d’une même variable quantitative, mais aussi pour analyser les données selon plusieurs facteurs. Dans cet article, nous aborderons uniquement le cas de l’Analyse de variance à un facteur. Nous expliquerons tout d’abord le principe de ce test, les formules de calcul de sa valeur globale et enfin la recherche de la p-value. Vous pouvez réaliser la globalité du test d’ANOVA sur MS Excel si vous êtes à l’aise avec cette application.
Sommaire
Les différentes utilités de l'ANOVA ?
Le test d’ANOVA à plusieurs utilités. Sans rentrer dans les détails de toutes les possibilités d’analyse fournit par ANOVA, nous expliquons dans ce paragraphe les deux grands tests.
En premier lieu, le test compare plusieurs séries de données, plus de deux, d’une même variable quantitative et de distribution normale. Par exemple comparer la perte de poids entre trois groupes de sujets ayant suivis 3 traitements différents A, B et C.
En deuxième lieu, l’analyse de variance ANOVA permet l’analyse les données selon plusieurs facteurs. Cela veut dire, que nous pouvons comparer des séries d’une même variable en fonctions d’autres variables de la base de données. C’est le cas par exemple de comparer l’effet de deux traitements pour la réduction de la Pression Artérielle (PA) en fonction de l’âge des patients.
Le premier facteur est le traitement dont la variable l’analyse sont les valeurs de la PA. Le deuxième facteur est l’âge des patients.
Dans quels cas utiliser ANOVA ?
Comme on pourrait penser que lorsque nous avons plusieurs groupes à comparer et que notre facteur d’interet est d’ordre quantitatif, nous pouvons utiliser le test T de Student. Ainsi nous povons faire des comparaisons de moyennes deux à deux. Cette approche est incorrecte et induit des erreurs. Nous expliquerons ci-dessous pourquoi nous ne devons pas utiliser le test T de Student pour des comparaisons multiples. Plus bas nous expliquerons comment faire une ANOVA pour une comparaison globale , puis utiliser des tests « Post-Hoc » pour des comparaisons deux à deux. Il est vrais que pour une comparaison de plus de deux groupes nous devons absolument passer par une comparaison globale d’ANOVA. L’utilisation des tests post hoc sont présentés dans un autre article.
ANOVA ou T de Student ?
Pour mieux comprendre la différence entre les deux tests, nous commençons par un petit exemple.
Nous envisageons lors d’une étude de comparer les moyennes de 3 groupes de sujets. La première étape consiste à poser les hypothèses de l’étude afin de la vérifier avec le test statistique adéquat:
Hypothèse nulle H0: Les moyennes « m » des 3 groupes sont égales: m1 =m2=m3 versus l’hypothèse alternative H1: Au moins une des 3 moyennes est différente des autres. Le risque d’erreur alpha est fixé à 5%.
La première idée qui nous vient à la tête c’est d’appliquer le test T (Student). Evidemment, le test T compare uniquement entre 2 moyennes.
A cet effet et dans le cas où nous devons comparer les moyennes deux à deux des trois groupes, nous devons donc tester 3 hypothèses.
- H0: m1 =m2 / H1 bilatérale : m1 ≠ m2 et
- H0: m2 =m3 / H1 bilatérale: m2 ≠ m3 et
- H0: m1 =m3/ H1 bilatérale: m1 ≠ m3 et
A chaque hypothèse posée, le niveau de confiance est fixé à 95%.
Seulement, avec trois hypothèses à tester, le niveau de confiance baisse. Il est égale à (0,95)³ = 0,857 et donc le risque d’erreur augmente.
Imaginons le cas de 4 comparaisons, le niveau de confiance sera égale à (0,95)6 = 0,735.
Et ainsi de suite, plus il y a de groupes à comparer plus le risque d’erreur augmente.
Pourtant, un test unique et global existe. C’est le test de Fisher-Snedecor d’ANOVA. Il est aussi possible de faire des comparaisons entre séries deux à deux avec des tests appelés « Post-Hoc » sans perte de confiance.
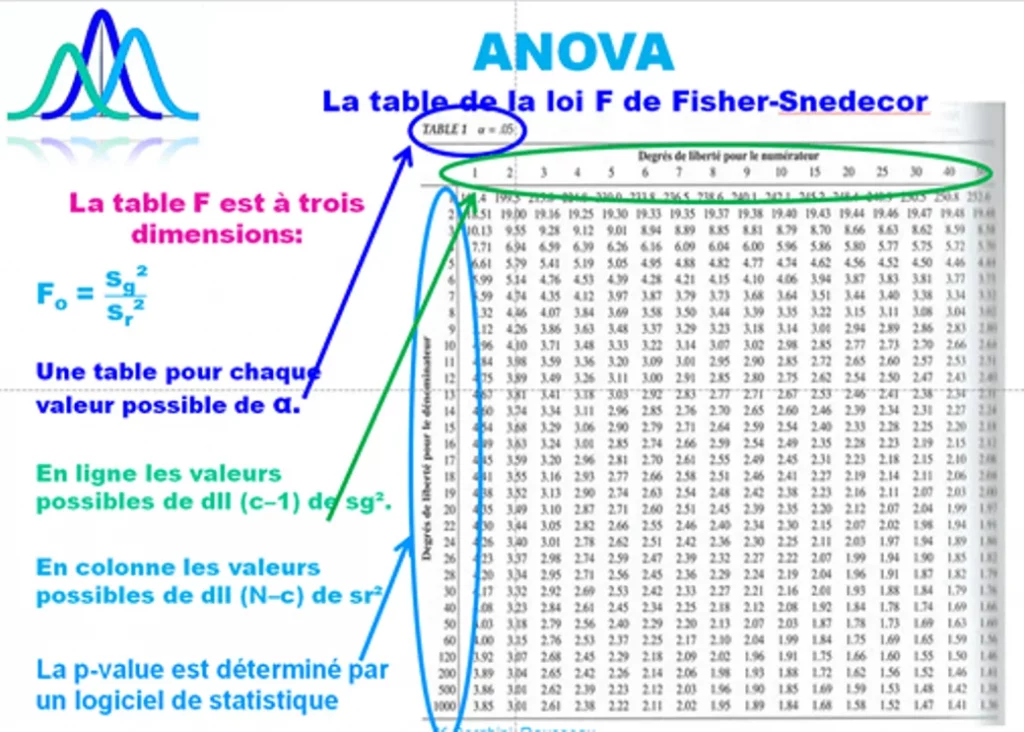
L’analyse de variance ANOVA est basée sur la loi F donc utilise la Table F de Fisher-Snedecor.
Le principe de l'analyse de variance ANOVA
Pour RAPPEL, la variance est la somme des carrés des écarts de chaque valeur (observation) à la valeur moyenne de l’échantillon sur le Nombre total des observations.
![]()
σ² = Somme des carrée (SC) des écarts / N ou σ² = Moyenne des carrés des écarts de chaque valeur à la valeur moyenne.
D’une manière générale, pour comparer entre les groupes, l’analyse de variance ANOVA test l’égalité de leurs moyennes en testant leurs variances.
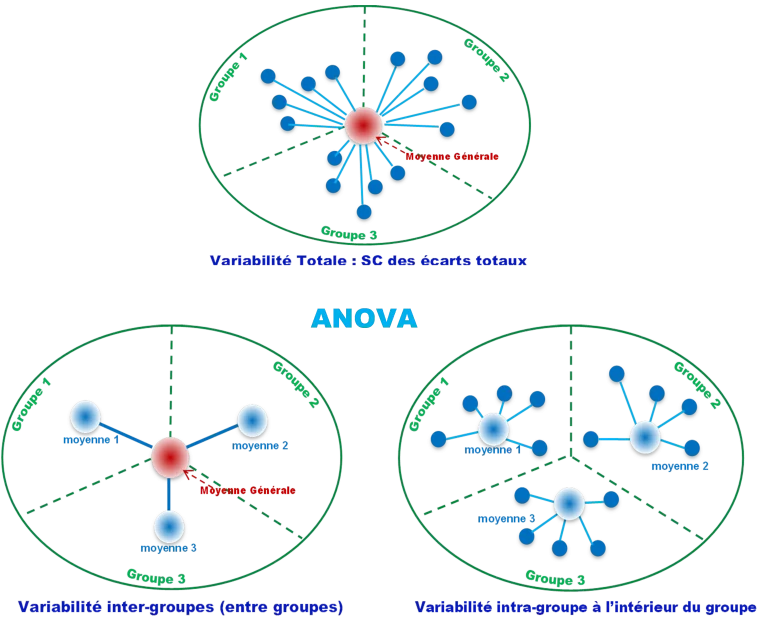
En réalité, elle détermine si les groupes varient de la même manière au sein de tout l’échantillon. En termes statistiques, l’ANOVA test la Variabilité Totale en déterminant la variation de chaque valeur du groupe (sa moyenne) à la moyenne générale Sc des écarts totaux dans le schéma ci-dessous.
Le test se réalise en deux étapes:
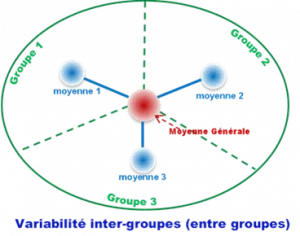
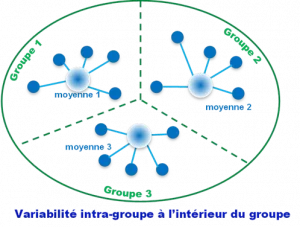
Premièrement, l’ANOVA calcul la variabilité entre les groupes ( Inter-groupe) (sg²) et la variabilité à l’intérieur de chaque groupe (intra-groupe) (sr²).
En deuxième étape, le test compare la variance Inter-groupe (sg²) à la variance Intra-groupe (sr²).
La variabilité Inter et Intra groupe
Commençant à examiner un exemple tout simple pour mieux comprendre entre la variabilité intra et Inter groupe. Dans l’exemple1 des tableaux ci-dessous, la variabilité entre les groupes sg² est nulle car les moyennes des 3 groupes sont égales. Par contre à l’intérieur de chaque groupe, les valeurs des observations sont différentes. Par conséquent, la variabilité intra-groupe est non nulle. Alors que pour l’exemple 2, la variabilité intra-groupe sr² est nulle =0 car les observations au sein de chaque groupes sont égales. Mais la variabilité sg² est non nulle car les moyennes des groupes sont différentes. Enfin dans l’exemple 3 la variabilité intra sr² et inter groupe sg² sont différentes de zéro.
Valeur du test d'Analyse de variance ANOVA
Comme expliqué plus haut, l’ANOVA compare globalement entre les différentes séries en calculant en un premier temps la variance inter-groupe sg² et intra-groupes (ou variance résiduelle) sr². Ensuite, elle compare ces deux grandeurs en calculant leur rapport:
F0 = sg² / sr².
F0 est la valeur du test de Fisher-Snedecor.
Avant de voir les détails des différents calculs du test F0, nous posons déjà les hypothèses de l’étude. Et comme vous le savez déjà, en analysant les données, nous vérifions toujours l’hypothèse nulle. Suite au résultat du test, soit nous acceptons, soit nous rejetons l’hypothèse nulle.
– Hypothèse nulle H0: la variabilité entre groupe est égale à la variabilité intra-groupe. Autrement dit, la variabilité est identique entre groupes et entre les individus de chaque groupe sg² = sr². Ce qui veut dire que toutes les moyennes testées sont identiques
– Versus l’hypothèse alternative H1: la variabilité entre les groupes est supérieure à la variabilité intra-groupe sg² > sr². En d’autres termes au moins une des moyennes est différente des autres.
Il faut souligner que dans le cas de l’analyse de variance, l’hypothèse alternative H1 est en approche unilatérale. Elle est à sens unique sg² > sr².
Les étapes de calcul de l'analyse de variance ANOVA
Nous détaillons ici les étapes de chaque calcul de variance ou variabilité intra et inter groupe. Ensuite, la valeur du test d’ANOVA ou valeur F0 qui va être comparé à une valeur théorique de la table de Fisher- Snédecor. Ces différentes formules ne devront pas vous impressionner. Elles sont très facilement calculables surtout sur MS Excel. Nous vous le démontrerons par un exemple à la fin de cet article.
1. Calcul de la variance inter-groupe ou entre groupes Sg²
La variance inter-groupe ou entre groupes Sg² , est la variation entre les groupes par mesure de l’écart moyen (SC des écarts / dll) entre chaque moyenne de groupe et la moyenne générale. SC = Somme des Carrées et dll est le degré de liberté.
Avec dll = c-1 et Sg² = (moy intra-groupe – moy globale)² x Moy Globale / dll
2. Variance intra-groupe ou variance résiduelle Sr²
La variance intra-groupe ou variance résiduelle sr² est la Somme des Carrés des écarts de chaque valeur à la valeur moyenne de son groupe sur le nombre d’individu dans le groupe.
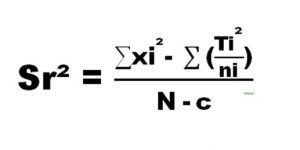
avec dll =N-C et Sr² : variance résiduelle (Intra-groupe) ou Sr² = SC intra-groupe / Nombre groupe x ddl total.
∑x²: Total des carrés des observations
3. Valeur du test d'ANOVA ou la valeur F de Fisher Snedecor
Pour calculer la valeur du test d’ANOVA, il suffit de faire le rapport de la variance inter-groupe sur la variance résiduelle (variance intra-groupe).
Avec les dlls: c – 1 et N – c
N: nombre total d’observation dans l’échantillon
c = Nombre de groupes à comparer
4. Comparaison de la valeur Fo et calcul de la p-value
La dernière étape, et comme pour tous les tests statistiques, il faut comparer la valeur calculée F0 à une valeur théorique F(α ; c -1; N – c) dans la table de la loi de Fisher-Snedecor. Mais nous pouvons tout à fait rechercher la p-value directement dans cette table. Dans tout les cas, deux cas se prèsentent:
Soit Fo < F(5%, c-1, N-c) ou p-value > 0,05, on accepte H0. Les moyennes sont égales ou ne différents pas significativement.
Soit Fo ≥ F(5% ; c-1; N-c) ou p-value ≤ 0,05 et dans ce cas on rejet de H0. Nous pouvons donc affirmer qu’au moins une des moyennes est significativement différente des autres.
Interprétations du résulat du test
Donc il faut comme même passer par les calculs d’une Analyse de variance ou au moins le calculs de la variance résiduelle pour pouvoir utiliser le test T.
Exemple d'application
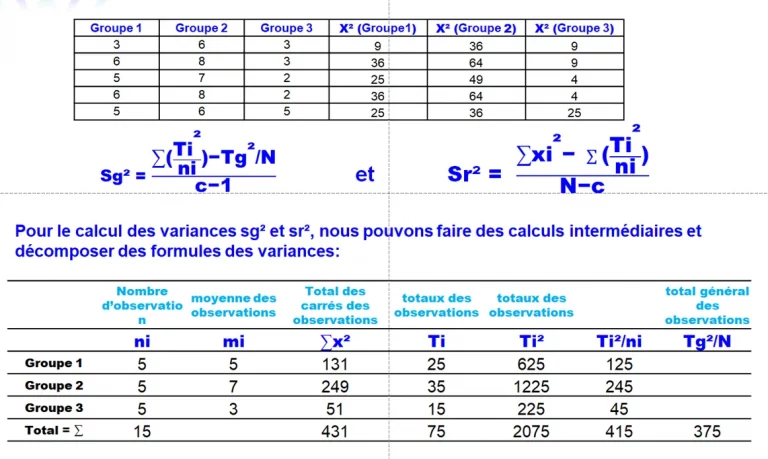
Nous présenterons les données de la table de l’exemple 3 ci-dessus pour illustrer les différentes étapes de calcul de l’ANOVA. Les calculs des variances Inter et Intra-groupes ne sont pas aussi compliqués et peuvent être réalisés sur Excel.
ni = Nombre d’observation ou effectifs dans chaque groupe.
mi = moyenne calculée dans chaque groupe.
∑x²: Total des carrés des observations dans chaque groupe.
Ti : Somme totale des observations de chaque groupe
Recherche de la p-value dans la table de Fisher-Snedecor
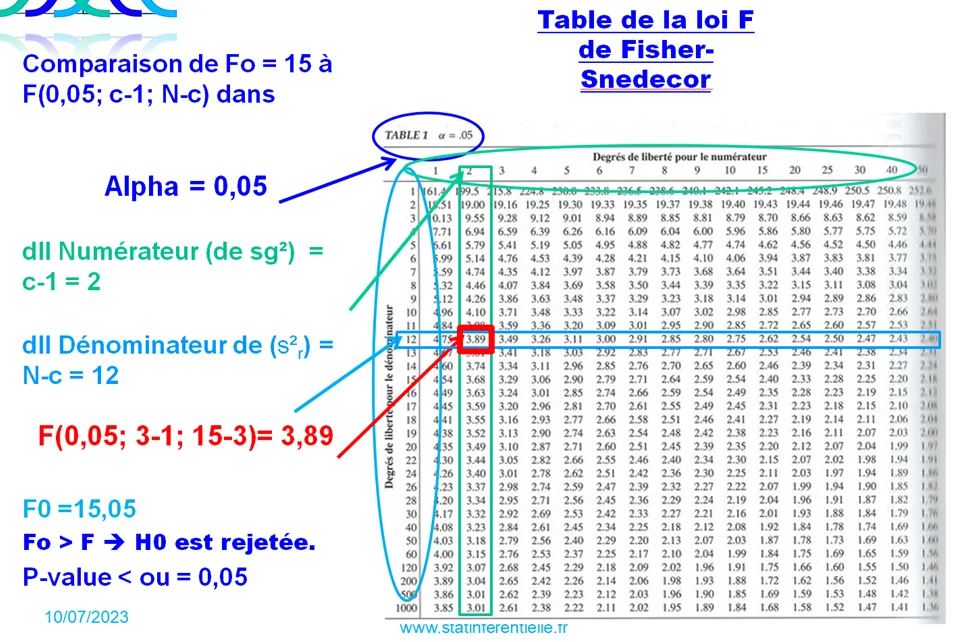
Donc la valeur du test Fo = sg²/sr² est égale à 15.
En interprétant cette valeur, nous pouvons dire que la variance Sg² inter-groupe est 15 fois plus grand que que la variance Sr² intra-groupe. Cela signifie que la variation entre les groupes est plus importante que la variation à l’interieure de chaque groupe (intra-groupe).
En plus, le ratio Fo est nettement supérieur à 3,89 de la table de Fisher F(0.05;2;12).
En conclusion de ce test et à un risque alpha de 5%, on rejette H0. H1 est vraie. Cequi veut dire que les moyennes des 3 groupes sont significativement différentes. Autrement dit, il y a au moins une moyenne d’un groupe qui différe significativement des autres.
Le test T de Student peut être utiliser pour comparer les moyennes entre elles deux à condition d’utiliser sr² comme variance commune.
Comparaison des résultats de l'analyse de variance ANOVA réalisée par un logiciel de Statistique
Si nous avons utiliser un logiciel statistique pour l’analyse des données de l’exemple 3, nous aurons le tableau d’ANOVA ci-dessou. Ainsi la sortie présente des différentes variances inter et intragroupes calculées, la valeur de F0 et bien sur la p-value. Evidement, un logiciel statistique donnera dirrectement la p-value.
Conditions d’application de l'analyse de variance ANOVA
Pour pouvoir appliquer l’analyse de variance ANOVA, il est important que les distributions des populations d’où proviennent les échantillons suivrent la loi Normale et d’égalité de variance.
Avant de procéder à une ANOVA, il convient donc de vérifier la normalité avec le test de Shapiro-Wilks ou le test de Kolmogorov-Smirnov ou par simple examination du diagramme quantile-quantile (ou « Q-Q plot). Ensuite, il faut tester l’homogénéité des variances (Homoscédasticité) avec le test de Bartlett ou le test de Levene.
Si la normalité des données n’est pas vérifiée, il faut utiliser un test non paramétrique équivalent tel que le test de Kruskall-Wallis.
A ce propos, le test de Kruskall-Wallis ayant le même principe que le test des rangs de Wilcoxon transforme les données en rangs.
Si cet article vous a été utile, Merci de le partager