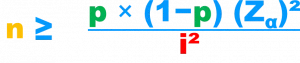Taille d'échantillon ou Nombre de sujets Nécessaires
Lorsqu’on construit une étude expérimentale pour évaluer un traitement ou étudier une caractéristique, nous devons recruter des sujets ou des patients afin de recueillir des données et les analyser. Mais pour pouvoir obtenir des résultats concluants, il faut déterminer en amont la taille d’échantillon ou calculer le Nombre de sujets nécessaires pour l’étude pour garantir une puissance suffisante des tests statistiques à réaliser.
Sommaire
Pourquoi déterminer la Taille d'échantillon lors d'une étude clinique ?
Prenant l’exemple d’une étude ou nous voulons comparer entre deux traitements. Pour cela, nous incluons arbitrairement 7 sujets par groupe. Après analyse, les résultats ne donnent aucune différence significative entre les deux groupes. Mais ces résultats, sont-ils réellement dus à une absence de différence entre les traitements? Très probablement non, ces résultats non concluants sont dus à un manque de puissance à cause du faible effectif de l’échantillon.
Cependant, il n’est pas non plus nécessaire d’inclure des centaines de sujets sans que cela ne soit justifié. Mais il suffit juste de déterminer le nombre de sujets nécessaires pour assurer une puissance suffisante des tests statistiques, tout en économisant sur les moyens humains, financiers et logistiques de l’étude.
Donc quand on bâtit une étude, il faut définir un nombre de sujets nécessaires et compatible avec les moyens dont on dispose, mais suffisamment grand pour assurer une validité des tests statistiques et leur puissance.
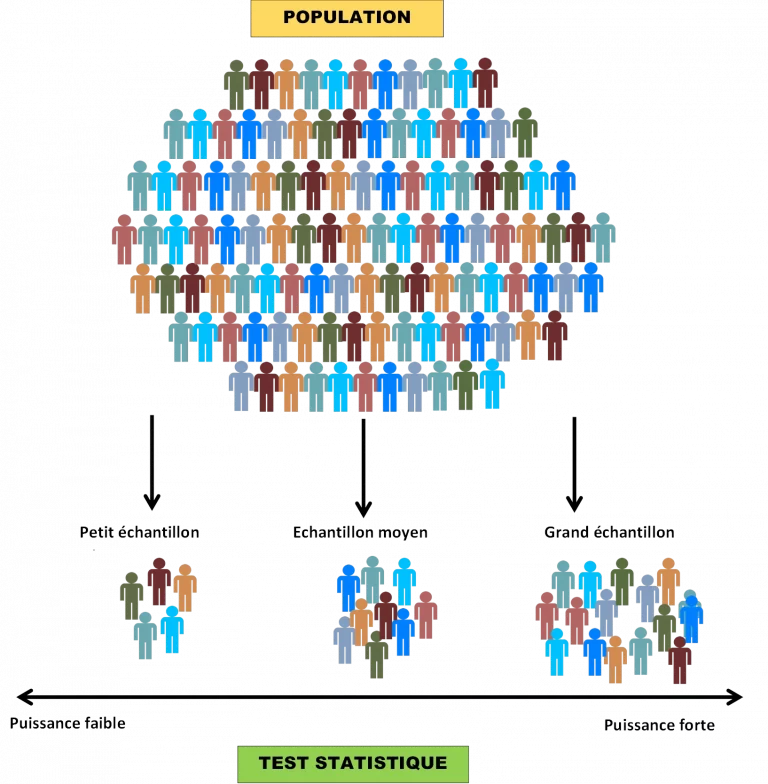
Taille d'échantillon et Puissance Statistique
Le risque d’erreur de deuxième espèce β
Nous avons assimilé la puissance d’un test statistique au pouvoir grossissant d’un microscope. Mais en réalité et de point de vue statistique, la puissance est une grandeur numérique définie par la valeur 1–β.
Au même titre que le risque Alpha α ou le risque de première espèce, il existe en effet un deuxième risque. C’est le risque d’erreur β ou risque de deuxième espèce. Ce dernier correspond au risque de conclure qu’il n’y a pas de différence entre deux populations alors qu’une différence existe belle et bien, mais qui n’a pas pu être démontrer par manque de puissance. Le risque β est donc le manque de puissance d’un test ou d’une analyse statistique et par conséquent, la valeur 1–β est la puissance statistique.
Les risques d’erreur α et β ainsi que la puissance sont mesurés en pourcentage.
Lors d’une étude expérimentale, le risque β est généralement fixé à 10% ou 20%, d’où pour une puissance suffisance, 1–β doit être choisie entre 80% et 90%.
La puissance et la Taille d’échantillon sont liés
Il faut savoir que ces deux grandeurs sont très liées. La puissance d’un test statistique est étroitement liée à la taille d’échantillon. Quand l’une augmente, l’autre augmente et inversement. Nous pouvons même déterminer la puissance du test connaissant la valeur de la taille de l’échantillon et Inversement.
De la même manière, quand la taille d’échantillon est grande, meilleure est la précision d’une estimation. Les écart types sont plus petits et l’Intervalle de Confiance IC est plus resserré. Vous pouvez consulter la définition et les explications de ces notions dans les articles dans notre blog.
Comment détermination la Taille d'échantillon de votre étude ?
Elements pour calculer le Nombre de sujets Nécessaires NSN
Pour calculer la Taille d’échantillon pour une étude, nous devons prendre en compte plusieurs facteurs :
Premièrement la variable du critère principal de l’étude
La détermination du nombre de sujets nécessaires se base sur le paramètre du premier critère à évaluer.
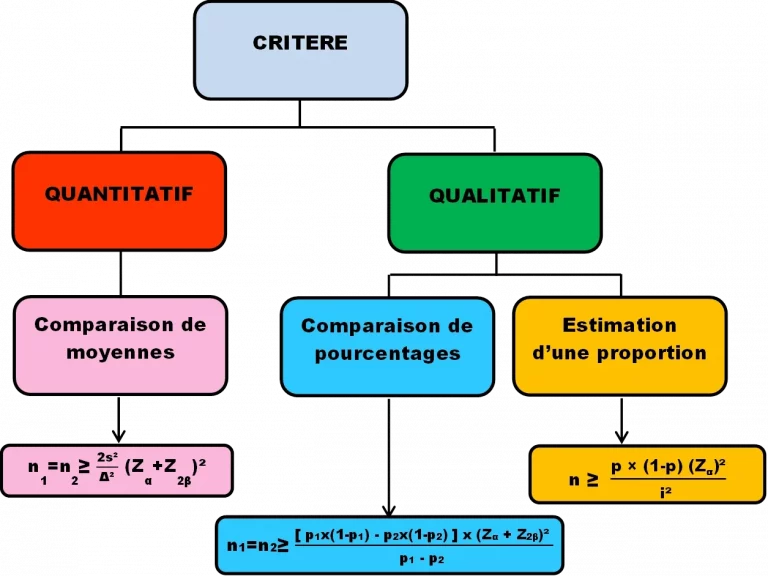
Plusieurs formules de calcul existent selon si ce critère est d’ordre quantitatif ou qualitatif ou selon la grandeur à comparer.
Il y a globalement trois formules de calcul. Pour la comparaison de deux moyennes, pour comparer entre deux pourcentages et pour l’estimation d’une proportion dans une population.
Deuxièmement il faut connaitre les valeurs attendues du paramètre étudié et son écart type
Pour chacun des deux groupes à comparer, Il faut avoir les valeurs moyennes ou les pourcentages des séries à comparer.
Par exemple, nous voulons comparer le taux de triglycéride entre deux groupes de patients (traité et contrôle). Pour calculer la taille de l’échantillon de cette étude, nous devons avoir la valeur moyenne du taux de triglycéride attendue ainsi que son écart type dans le groupe traité et dans le groupe contrôle. Ou la différence de moyenne attendue entre les deux groupes, c’est la valeur delta Δ.
Troisièmement: fixer le risque α et la puissance désirée
Nous devons déterminer le risque d’erreur de première espèce alpha α. Si vous avez déjà regardé cet article, vous saurez que ce risque est fixé à priori et géréralement à 5%. Puis décider d’une puissance suffisante qui doit être normalement entre 80% et 90%.
Comment trouver les valeurs du paramètre pour le calcul de la Taille d’un échantillon ?
Souvent, les valeurs (moyennes, pourcentages ou leurs différences ainsi que les écarts types) du critère étudié sont inconnues. Nous faisons justement l’étude pour les déterminer. Mais nous pouvons les estimer en cherchant leurs valeurs les plus proches soit:
- Sur nos connaissances préliminaires sur le sujet.
- Par des études pilotes. Se sont des petites études menées avec un petit effectif de sujets pour déterminer les valeurs du critère étudié.
- Dans les résultats des publications scientifiques dont le sujet est très proche du sujet étudié.
Une fois que tous ces éléments sont connus, nous appliquerons l’une des formules de calcul ci-dessous, bien sur celle qui s’adapte le mieux à notre plan expérimental.
Formules de calcul de la Taille d'un échantillon
Comparaison de deux moyennes, cas d'un test T de Student
n1 = n2 : Nombre de sujets nécessaires de chaque groupe à comparer dans l’échantillon.
Δ : Le delta ou la différence attendue entre les deux moyennes à comparer. Δ = m1 -m2
s² : La variance notée aussi σ² de la population dont sont issus les échantillons. Cette variance doit être estimée sur des connaissances préalables.
Zα : Valeur au risque α de 5% en hypothèse bilatérale, Zα = 1,96.
Z2β : Valeur au risque β de 20% de la Table Z, Z2β = 0,842.
Exemple1. Détermination de la taille de l’échantillon pour comparer deux moyennes
On veut comparer le poids de 2 groupes de sujets d’effectifs égaux. Nous voulons savoir combien de sujets il faut inclure dans chaque groupe pour espérer observer une différence de moyenne de 3 kg avec un risque d’erreur α de 5% et une puissance de 80%. On estime que l’écart type dans la population générale est de 4 kg.<br>
– Le critère principal est le poids en kg
– Delta Δ = 3 kg. L’écart type = 4 kg d’où la variance de différence de poids est s²= 16 kg.
– Puissance 1- β = 80% ou β = 20% d’où Z2β = 0,842.
– Risque α avec Hypothèse en bilatérale d’où Z(5%) = 1,96.
n1 = n2 = 2 x (4²) x (1,96 + 0,842)² / 3² = 27,92
Soit en pratique il faut inclure au moins 28 sujets par groupe. Et au total nous devons inclure au moins 56 sujets dans cette étude.
Comparaison de deux pourcentages, cas d'un Khi-deux
n1 = n2 : Nombre de sujet nécessaire de chaque groupe de l’échantillon.
p1 et p2 : Pourcentages des deux groupes à comparer.
Nous estimons ces valeurs dans des études comparables ou dans la bibliographie.
Zα : au risque α de 5%, Zα = 1,96.
Z2β : au risque β de 20%, Z2β = 0,842.
Estimation d'une proportion
n = Taille de l’échantillon
p = Pourcentage de la variable qualitative dans la population. Ce pourcentage est inconnu puisque l’on réalise l’étude pour le déterminer. On l’estime par des études comparables ou dans la bibliographie.
i = La précision désirée. Exemple si on veut estimer le % de sujet malade, on peut demander une précision de 4%.
Zα : au risque α de 5%, Zα = 1,96.
Exemple2. Calcul du nombre de sujets nécessaires pour estimer un pourcentage
On désire estimer la proportion de trouble de la concentration chez les enfants de 6 à 12 ans d’un département français. Des études antérieures pratiquées dans d’autres régions montrent que la proportion de ces troubles est d’environ 16%. On désire une précision de ± 3% et on choisit un risque de 5%.
Quel est le nombre d’enfants à inclure dans l’étude ?
La précision i = 3% ; i² = (0,03)² = 0,0009.
Pourcentage de trouble estimé p = 16% d’où p (1 – p) = 0,16 (1-0,16) = 0,134
Risque α en hypothèse bilatérale : Z(5%) = 1,96.
n = 0,1344 / 0,0009 * (1,96)² = 574.
il faut donc inclure au moins 574 enfants pour cette étude.
Pour résumer
Si vous avez à calculer le nombre de sujets nécessaire pour votre étude, vous pouvez soit utiliser les formules ci-dessus ou bien utiliser un logiciel de calcul. Dans les deux cas et pour mettre en évidence une différence significative en termes d’efficacité d’un produit, il faut tenir compte des 4 paramètres obligatoires pour le calcul de la taille de l’échantillon:
Choix du risque α (en général 5%) ce qui correspond à Zα = 1,96.
Choisir la puissance désirée (en général 80%) et donc le risque β (20%) ou Z2β = 0,842.
Se fixer une différence minimale Delta (Δ) entre les paramètres à comparer. En général plus la différence Delta (Δ) à démontrer est faible, plus la taille de l’échantillon sera élevée.
Estimer une variance de cette différence. Ce paramètre est délicat car inconnu avant l’étude. Il faut utiliser les résultats d’autres études antérieures ou de la bibliographie ou lors d’une étude pilote.
Si cet article vous a été utile, Merci de le partager